题目内容
1.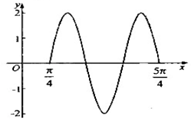 已知函数f(x)=2sin(ωx+φ),(ω>0,0≤φ<2π)的部分图象如图所示,则f(x)=2sin(3x+$\frac{5π}{4}$).
已知函数f(x)=2sin(ωx+φ),(ω>0,0≤φ<2π)的部分图象如图所示,则f(x)=2sin(3x+$\frac{5π}{4}$).
分析 根据函数f(x)的部分图象,求出最小正周期T、ω以及φ的值即可.
解答 解:根据函数f(x)=2sin(ωx+φ)的部分图象知,
$\frac{3T}{2}$=$\frac{5π}{4}$-$\frac{π}{4}$=π
∴T=$\frac{2π}{3}$,∴ω=$\frac{2π}{T}$=3,
根据五点法画图知,ω•$\frac{π}{4}$+φ=$\frac{3π}{4}$+φ=2kπ,k∈Z,
解得φ=2kπ-$\frac{3π}{4}$,k∈Z,
∵0≤φ<2π,
∴φ=$\frac{5π}{4}$,
∴f(x)=2sin(3x+$\frac{5π}{4}$).
故答案为:2sin(3x+$\frac{5π}{4}$).
点评 本题考查了由y=Asin(ωx+φ)的部分图象确定解析式的应用问题,是基础题目.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
12.在△ABC中,“sinA=sinB”是“A=B”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.若x>0,y>0,且$\frac{1}{x}+\frac{1}{y}=\frac{1}{2}$,则xy有( )
| A. | 最大值16 | B. | 最小值$\frac{1}{16}$ | C. | 最小值16 | D. | 最小值$\frac{1}{2}$ |
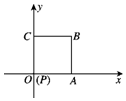 如图放置的边长为2的正方形PABC沿x轴正半轴滚动.设顶点P(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为8;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为4π+4.
如图放置的边长为2的正方形PABC沿x轴正半轴滚动.设顶点P(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为8;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为4π+4.