Question

已知函数f（x）=

2x-a，x≥0 x2+ax+a，x＜0

有三个不同的零点，则实数a的取值范围是

 

．

Answer 1

考点：根的存在性及根的个数判断

专题：函数的性质及应用

分析：由题意可得函数f（x）的图象与x轴有三个不同的交点，结合图象求出实数a的取值范围．

解答： 解：由题意可得函数f（x）的图象与x轴有三个不同的交点，
函数f（x）=

2x-a，x≥0 x2+ax+a，x＜0

的图象如图所示：

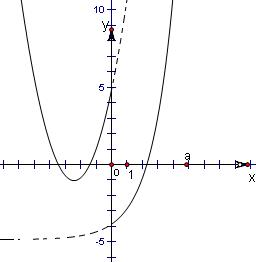
由图可知，函数f（x）=

2x-a，x≥0 x2+ax+a，x＜0

有三个不同的零点等价于：
当x≥0时，方程2^x-a=0有一个根，且x＜0时，方程x²+ax+a=0有两个根，
即

a＞0 △=a2-4a＞0

，
解得：a＞4．
故实数a的取值范围是a＞4．
故答案为：a＞4．

点评：本题主要考查函数的零点与方程的根的关系，体现了化归与转化、数形结合的数学思想，属于中档题．