题目内容
 已知函数f(x)=x2-2x+4
已知函数f(x)=x2-2x+4(1)作出函数f(x)的图象;
(2)指出函数f(x)的单调递增区间,并用单调性的定义证明;
(3)求函数y=f(x),x∈[t,t+1]的最小值.
考点:函数的图象,二次函数的性质,二次函数在闭区间上的最值
专题:函数的性质及应用
分析:(1)列表描点连线即可得出函数的图象,
(2)先由图象得到函数的单调区间,再利用定义证明即可,
(3)进行分类讨论,得到函数耳朵最小值.
(2)先由图象得到函数的单调区间,再利用定义证明即可,
(3)进行分类讨论,得到函数耳朵最小值.
解答:
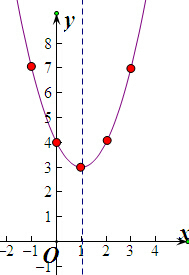 解:(1)列表
解:(1)列表
描点连线图象如图所示,
(2)由图象可知,函数f(x)在(-∞,1)上单调递减,在(1,∞)上单调递增,
理由如下,设x1,<x2∈((-∞,1),则f(x1)-f(x2)=x12-2x1+4-(x22-2x2+4)=x12-2x1-x22+2x2=(x1+x2)(x1-x2)-2(x1-x2)=(x1-x2)((x1+x2)-2),
∵x1,<x2∈((-∞,1),
∴x1-x2<0,(x1+x2)-2<0,
∴f(x1)-f(x2)>0,
∴函数f(x)在(-∞,0)上单调递减,
同理可证函数f(x)在(1,∞)上单调递增,
(3)当t≥1时,函数f(x)在∈[t,t+1]上单调递增,故f(x)min=f(t)=3t2-2t+4,
当t≤0时,函数f(x)在∈[t,t+1]上单调递减,故f(x)min=f(t+1)=3(t+1)2-2(t+1)+4=3t2+4t+5,
当0<t<1时,f(x)min=f(1)=3,
 解:(1)列表
解:(1)列表 | x | … | -1 | 0 | 1 | 2 | 3 | … |
| f(x) | … | 7 | 4 | 3 | 4 | 7 | … |
(2)由图象可知,函数f(x)在(-∞,1)上单调递减,在(1,∞)上单调递增,
理由如下,设x1,<x2∈((-∞,1),则f(x1)-f(x2)=x12-2x1+4-(x22-2x2+4)=x12-2x1-x22+2x2=(x1+x2)(x1-x2)-2(x1-x2)=(x1-x2)((x1+x2)-2),
∵x1,<x2∈((-∞,1),
∴x1-x2<0,(x1+x2)-2<0,
∴f(x1)-f(x2)>0,
∴函数f(x)在(-∞,0)上单调递减,
同理可证函数f(x)在(1,∞)上单调递增,
(3)当t≥1时,函数f(x)在∈[t,t+1]上单调递增,故f(x)min=f(t)=3t2-2t+4,
当t≤0时,函数f(x)在∈[t,t+1]上单调递减,故f(x)min=f(t+1)=3(t+1)2-2(t+1)+4=3t2+4t+5,
当0<t<1时,f(x)min=f(1)=3,
点评:本题主要考查了函数的图象单调性,最值,属于基础题.

练习册系列答案
相关题目
已知集合A={x||x|<2},B={x|
<2x<8},则A∩B=( )
| 1 |
| 2 |
| A、{x|-1<x<2} |
| B、{x|-1<x<3} |
| C、{x|-2<x<3} |
| D、{x|-2<x<2} |
 如图所示,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.
如图所示,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.