题目内容
为了解某高中学生视力情况,现从该高中随机抽取20名学生,经校医检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如图示;
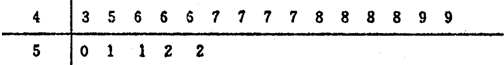
(1)若视力测试缩果不低于5.0,则称为“健康视力”,求校医从这20人中随机选取3人,至多有1人是“健康枧力”的概率;
(2)以这20人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记ξ表示抽到“健康视力”学生的人数,求ξ的分布列及数学期望.
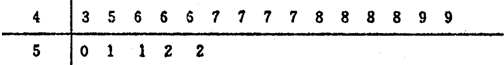
(1)若视力测试缩果不低于5.0,则称为“健康视力”,求校医从这20人中随机选取3人,至多有1人是“健康枧力”的概率;
(2)以这20人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记ξ表示抽到“健康视力”学生的人数,求ξ的分布列及数学期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:概率与统计
分析:(1)设Ai表示所取3人中有i(i=0,1)个人是“健康视力”,至多有1人是“健康视力”记为事件A,则P(A)=P(A0)+P(A1),由此能求出至多有1人是“健康枧力”的概率.
(2)由题意知ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列及数学期望.
(2)由题意知ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列及数学期望.
解答:
解:(1)设Ai表示所取3人中有i(i=0,1)个人是“健康视力”,
至多有1人是“健康视力”记为事件A,
则P(A)=P(A0)+P(A1)=
+
=
.
(2)由题意知ξ的可能取值为0,1,2,3,
P(ξ=0)=(
)3=
,
P(ξ=1)=
×
×(
)2=
,
P(ξ=2)=
×(
)2×
=
,
P(ξ=3)=(
)3=
,
ξ的分布列为:
∴Eξ=0×
+1×
+2×
+3×
=
.
至多有1人是“健康视力”记为事件A,
则P(A)=P(A0)+P(A1)=
| ||
|
| ||||
|
| 49 |
| 57 |
(2)由题意知ξ的可能取值为0,1,2,3,
P(ξ=0)=(
| 3 |
| 4 |
| 27 |
| 64 |
P(ξ=1)=
| C | 1 3 |
| 1 |
| 4 |
| 3 |
| 4 |
| 27 |
| 64 |
P(ξ=2)=
| C | 2 3 |
| 1 |
| 4 |
| 3 |
| 4 |
| 9 |
| 64 |
P(ξ=3)=(
| 1 |
| 4 |
| 1 |
| 64 |
ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 27 |
| 64 |
| 27 |
| 64 |
| 9 |
| 64 |
| 1 |
| 64 |
| 3 |
| 4 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期的望的求法,解题时要认真审题,是中档题.

练习册系列答案
相关题目
 如图所示,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.
如图所示,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.