题目内容
3.某厂生产某种新产品x件的总成本:C(x)=1200+$\frac{2}{75}$x3,又产品单价的平方与产品件数x成反比,生产100件这样的产品的单价为50元,总利润最大时,产量应定为( )| A. | 25件 | B. | 20件 | C. | 15件 | D. | 30件 |
分析 分析题目数据建立数学模型,得出总利润函数L(x)=$\frac{500}{\sqrt{x}}$•x-(1200+$\frac{2}{75}$x3)(x>0),注意定义域,然后利用导数求其最值,还原为实际问题即可.
解答 解:解:设产品单价为p,则有p2=$\frac{k}{x}$,
将x=100,p=50代入,得k=250000,
所以p=p(x)=$\frac{500}{\sqrt{x}}$,
设总利润为L,L=L(x)=p(x)-c(x)=$\frac{500}{\sqrt{x}}$•x-(1200+$\frac{2}{75}$x3)(x>0),
即L(x)=$\frac{500}{\sqrt{x}}$•x-1200-$\frac{2}{75}$x3,L'(x)=$\frac{250}{\sqrt{x}}$-$\frac{2{x}^{2}}{25}$,
令L'(x)=0,即$\frac{250}{\sqrt{x}}$-$\frac{2{x}^{2}}{25}$=0,解得x=25,
因为x=25是函数L(x)在(0,+∞)上唯一的极值点,
且是极大值点,从而是最大值点.
故选:A.
点评 本题考查利用导数解决生活中的优化问题的方法和步骤,属于中档题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
8.若x∈(1,a),则M=logax2,N=loga2x的大小关系是( )
| A. | M<N | B. | M>N | C. | M=N | D. | 不能确定 |
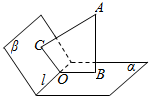 如图所示,在二面角α-l-β内有一点A,过A作AB⊥α于B,作AC⊥β于C,如果∠BAC=25°,那么二面角α-l-β是多少度.
如图所示,在二面角α-l-β内有一点A,过A作AB⊥α于B,作AC⊥β于C,如果∠BAC=25°,那么二面角α-l-β是多少度.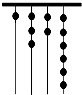 原始社会时期,人们通过在绳子上打结来计算数量,即“结绳计数”,当时有位父亲,为了准确记录孩子的成长天数,在粗细不同的绳子上打结,由细到粗,满七进一,那么孩子已经出生多少天?( )
原始社会时期,人们通过在绳子上打结来计算数量,即“结绳计数”,当时有位父亲,为了准确记录孩子的成长天数,在粗细不同的绳子上打结,由细到粗,满七进一,那么孩子已经出生多少天?( )