题目内容
12．
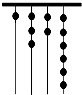原始社会时期，人们通过在绳子上打结来计算数量，即“结绳计数”，当时有位父亲，为了准确记录孩子的成长天数，在粗细不同的绳子上打结，由细到粗，满七进一，那么孩子已经出生多少天？（ ）| A． | 1326 | B． | 510 | C． | 429 | D． | 336 |
分析 由题意可得，该表示为七进制，运用进制转换，即可得到所求的十进制数．
解答 解：由题意满七进一，可得该图示为七进制数，
化为十进制数为1×73+3×72+2×7+6=510．
故选：B．
点评 本题考查计数的方法，注意运用七进制转化为十进制数，考查运算能力，属于基础题．
练习册系列答案
相关题目
2．登山运动是一项有益身心健康的活动，但它受山上气温的限制．某登山爱好者为了了解某山上气温y（℃）与相应山高x（km）之间的关系，随机统计了5次山上气温与相应山高，如下表：
（1）根据上表数据，用最小二乘法求出y关于x的线性回归方程：$\widehat{y}$=bx+$\widehat{a}$；
（2）若该名登山者携带物品足以应对山上-2.4℃的环境，试根据（1）中求出的线性回归方程预测，这名登山者最高可以攀登到多少千米处？
（参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{i}（{x}_{n}-\overline{x}）^{2}}$，$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$）
| 气温y（℃） | 18 | 16 | 10 | 4 | 2 |
| 山高（km） | 2.6 | 3 | 3.4 | 4.2 | 4.8 |
（2）若该名登山者携带物品足以应对山上-2.4℃的环境，试根据（1）中求出的线性回归方程预测，这名登山者最高可以攀登到多少千米处？
（参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{i}（{x}_{n}-\overline{x}）^{2}}$，$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$）
3．某厂生产某种新产品x件的总成本：C（x）=1200+$\frac{2}{75}$x3，又产品单价的平方与产品件数x成反比，生产100件这样的产品的单价为50元，总利润最大时，产量应定为（ ）
| A． | 25件 | B． | 20件 | C． | 15件 | D． | 30件 |
7．若A、B、C是△ABC的三个内角，则（ ）
| A． | sinA=sin（B+C） | B． | cosA=cos（B+C） | C． | tanA=tan（B+C） | D． | cotA=cot（B+C） |
17．在△ABC中，a=4，b=4，C=30°，则c2等于（ ）
| A． | 32-16$\sqrt{3}$ | B． | 32+16$\sqrt{3}$ | C． | 16 | D． | 48 |