题目内容
13.设f(x)=$\left\{\begin{array}{l}{{2}^{-x}-1,x≤0}\\{{x}^{\frac{1}{2}},x>0}\end{array}\right.$,若x满足f(x)≥3,则log2($\frac{x+1}{x-1}$)的最大值为log2$\frac{5}{4}$.分析 先求出满足f(x)≥3的x的范围,再求出t=$\frac{x+1}{x-1}$的范围,结合对数函数的图象和性质,可得答案.
解答 解:当x≤0时,由2-x-1≥3得:x≤-2,
当x>0时,由${{x}^{\frac{1}{2}}}_{\;}$≥3得:x≥9,
故t=$\frac{x+1}{x-1}$=1+$\frac{2}{x-1}$∈[$\frac{1}{3}$,1)∪(1,$\frac{5}{4}$],
故log2($\frac{x+1}{x-1}$)的最大值为log2$\frac{5}{4}$,
故答案为:log2$\frac{5}{4}$
点评 本题考查的知识点是分段函数的应用,反比例型函数的图象和性质,对数函数的图象和性质,难度中档.

练习册系列答案
相关题目
4. 为了检查某高三毕业班学生的体重状况,从该班随机抽取了10位学生进行称重,如图为10位学生体重的茎叶图,其中图中左边是体重的十位数字,右边是个位数字,则这10位学生体重的平均数与中位数之差为( )( )
为了检查某高三毕业班学生的体重状况,从该班随机抽取了10位学生进行称重,如图为10位学生体重的茎叶图,其中图中左边是体重的十位数字,右边是个位数字,则这10位学生体重的平均数与中位数之差为( )( )
 为了检查某高三毕业班学生的体重状况,从该班随机抽取了10位学生进行称重,如图为10位学生体重的茎叶图,其中图中左边是体重的十位数字,右边是个位数字,则这10位学生体重的平均数与中位数之差为( )( )
为了检查某高三毕业班学生的体重状况,从该班随机抽取了10位学生进行称重,如图为10位学生体重的茎叶图,其中图中左边是体重的十位数字,右边是个位数字,则这10位学生体重的平均数与中位数之差为( )( )| A. | 0.1 | B. | 0.2 | C. | 0.3 | D. | 0.4 |
1.下列方程可表示圆的是( )
| A. | x2+y2+2x+3y+5=0 | B. | x2+y2+2x+3y+6=0 | C. | x2+y2+2x+3y+3=0 | D. | x2+y2+2x+3y+4=0 |
18.若函数f(x)=ax3-2x2在x=-1时取得极值,则f(1)等于( )
| A. | -$\frac{10}{3}$ | B. | -$\frac{2}{3}$ | C. | 0 | D. | $\frac{1}{3}$ |
2.登山运动是一项有益身心健康的活动,但它受山上气温的限制.某登山爱好者为了了解某山上气温y(℃)与相应山高x(km)之间的关系,随机统计了5次山上气温与相应山高,如下表:
(1)根据上表数据,用最小二乘法求出y关于x的线性回归方程:$\widehat{y}$=bx+$\widehat{a}$;
(2)若该名登山者携带物品足以应对山上-2.4℃的环境,试根据(1)中求出的线性回归方程预测,这名登山者最高可以攀登到多少千米处?
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{i}({x}_{n}-\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$)
| 气温y(℃) | 18 | 16 | 10 | 4 | 2 |
| 山高(km) | 2.6 | 3 | 3.4 | 4.2 | 4.8 |
(2)若该名登山者携带物品足以应对山上-2.4℃的环境,试根据(1)中求出的线性回归方程预测,这名登山者最高可以攀登到多少千米处?
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{i}({x}_{n}-\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$)
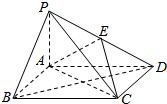 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,AP=1,AD=$\sqrt{3}$,PA⊥平面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,AP=1,AD=$\sqrt{3}$,PA⊥平面ABCD,E为PD的中点.