题目内容
11.已知集合M={-3,-2,-1,0,1,2},P(a,b)表示平面上的点(a,b∈M),(1)P可以表示平面上的多少个不同点?
(2)P可以表示平面上的多少个第二象限的点?
(3)P可以表示多少个不在直线y=x上的点?
分析 利用列举法求解.
解答 解:(1)∵集合M={-3,-2,-1,0,1,2},P(a,b)表示平面上的点(a,b∈M),
∴P点的可能坐标有:
(-3,-2),(-2,-3),(-3,-1),(-1,-3),(-3,0),(0,-3),(-3,1),(1,-3),
(-3,2),(2,-3),(-2,-1),(-1,-2),(-2,0),(0,-2),(-2,1),(1,-2),
(-2,2),(2,-2),(-1,0),(0,-1),(-1,1),(1,-1),(-1,2),(2,-1),(0,1),
(1,0),(0,2),(2,0),(1,2),(2,1),(-3,-3),(-2,-2),(-1,-1),(0,0),(1,1),(2,2),共36个.
(2)P表示平面上的第二象限的点有:
(-3,1),(-3,2),(-2,1),(-2,2),(-1,1),(-1,2),共6个.
(3)P可以表示不在直线y=x上的点有:
(-3,-2),(-2,-3),(-3,-1),(-1,-3),(-3,0),(0,-3),(-3,1),(1,-3),
(-3,2),(2,-3),(-2,-1),(-1,-2),(-2,0),(0,-2),(-2,1),(1,-2),
(-2,2),(2,-2),(-1,0),(0,-1),(-1,1),(1,-1),(-1,2),(2,-1),(0,1),
(1,0),(0,2),(2,0),(1,2),(2,1),共30个.
点评 本题考查元素个数的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.10名工人某天生产同一零件,生产的件数是15,17,14,10,17,17,16,14,12,10,设平均数为a,中位数为b,众数为c,则有( )
| A. | a>b>c | B. | b>c>a | C. | c>a>b | D. | c>b>a |
1.已知非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$$-\overrightarrow{b}$|=3|$\overrightarrow{b}$|,则cos<$\overrightarrow{a}$,$\overrightarrow{b}$$-\overrightarrow{a}$>=( )
| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{2\sqrt{2}}{3}$ | D. | -$\frac{1}{3}$ |
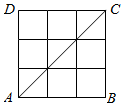 如图,ABCD为边长为3的正方形,把各边三等分后,共有16个交点,从中选取两个交点作为向量,则与$\overrightarrow{AC}$平行且长度为2$\sqrt{2}$的向量个数有8个.
如图,ABCD为边长为3的正方形,把各边三等分后,共有16个交点,从中选取两个交点作为向量,则与$\overrightarrow{AC}$平行且长度为2$\sqrt{2}$的向量个数有8个.