题目内容
16.复数$\frac{(-1+\sqrt{3}i)^{5}}{1+\sqrt{3}i}$的值是( )| A. | -16 | B. | 16 | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$-$\frac{\sqrt{3}}{4}$i |
分析 $(-\frac{1}{2}+\frac{\sqrt{3}}{2}i)^{2}$=$-\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i,$(-\frac{1}{2}+\frac{\sqrt{3}}{2}i)^{3}$=1.代入即可得出.
解答 解:∵$(-\frac{1}{2}+\frac{\sqrt{3}}{2}i)^{2}$=$-\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i,$(-\frac{1}{2}+\frac{\sqrt{3}}{2}i)^{3}$=1.
$\frac{(-1+\sqrt{3}i)^{5}}{1+\sqrt{3}i}$=$\frac{{2}^{5}(-\frac{1}{2}+\frac{\sqrt{3}}{2}i)^{5}}{2(\frac{1}{2}+\frac{\sqrt{3}}{2}i)}$=$\frac{{2}^{4}(-\frac{1}{2}-\frac{\sqrt{3}}{2}i)}{\frac{1}{2}+\frac{\sqrt{3}}{2}i}$=-16.
故选:A.
点评 本题考查了复数的运算法则、共轭复数的定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.已知点P是以F1,F2为焦点的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>0,b>0})$上一点,若$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=0,tan∠P{F_1}{F_2}=\frac{1}{3}$,则椭圆的离心率是( )
| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{10}}}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
10.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2$\sqrt{2}$,若直线y=-$\sqrt{3}$(x+$\sqrt{2}$)与椭圆交于点M,满足$\frac{1}{2}$∠MF1F2=∠MF2F1,则离心率是( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{3}$-1 | C. | $\frac{{\sqrt{3}-1}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
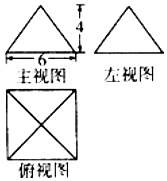 已知某几何体的三视图如图所示,俯视图是正方形,正视图和侧视图都是底面边长为6,高为4的等腰三角形.
已知某几何体的三视图如图所示,俯视图是正方形,正视图和侧视图都是底面边长为6,高为4的等腰三角形.