题目内容
3.已知(1-x)n的展开式中,前三项的二项式系数之和是22,求展开式中的中间项.分析 根据(1-x)n展开式的前三项的二项式系数和列出方程求出n的值,再求展开式的中间项.
解答 解:(1-x)n的展开式中,前三项的二项式系数之和是22,
∴${C}_{n}^{0}$+${C}_{n}^{1}$+${C}_{n}^{2}$=22,
即1+n+$\frac{1}{2}$n(n-1)=22,
化简得n2+n-42=0,
解得n=6或n=-7(不合题意,舍去),
∴(1-x)6展开式的中间项为
T4=${C}_{6}^{3}$•(-x)3=-20x3.
点评 本题考查了二项式定理的应用问题,也考查了转化思想与解方程的应用问题,是基础题目.

练习册系列答案
相关题目
13.函数y=${3^{\sqrt{x}}}$的值域为( )
| A. | (0,+∞) | B. | [1,+∞) | C. | [3,+∞) | D. | [9,+∞) |
14.点P(2,0)关于直线x+y+1=0对称点Q的坐标为( )
| A. | (-1,-3) | B. | (3,3) | C. | (-1,3) | D. | (4,-2) |
11.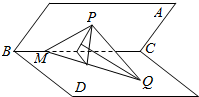 如图所示,二面角A-BC-D的大小为45°,P为平面ABC内一点,Q为平面BCD内一点,M为BC上一点,已知P在平面BCD内的射影恰好在线段MQ上,设PM=$\sqrt{2}$,∠CMQ=45°,直线PQ与平面BCD所成的角为30°,则PQ的长为( )
如图所示,二面角A-BC-D的大小为45°,P为平面ABC内一点,Q为平面BCD内一点,M为BC上一点,已知P在平面BCD内的射影恰好在线段MQ上,设PM=$\sqrt{2}$,∠CMQ=45°,直线PQ与平面BCD所成的角为30°,则PQ的长为( )
 如图所示,二面角A-BC-D的大小为45°,P为平面ABC内一点,Q为平面BCD内一点,M为BC上一点,已知P在平面BCD内的射影恰好在线段MQ上,设PM=$\sqrt{2}$,∠CMQ=45°,直线PQ与平面BCD所成的角为30°,则PQ的长为( )
如图所示,二面角A-BC-D的大小为45°,P为平面ABC内一点,Q为平面BCD内一点,M为BC上一点,已知P在平面BCD内的射影恰好在线段MQ上,设PM=$\sqrt{2}$,∠CMQ=45°,直线PQ与平面BCD所成的角为30°,则PQ的长为( )| A. | $\frac{2}{3}\sqrt{6}$ | B. | $\frac{3}{4}\sqrt{6}$ | C. | $\frac{4}{3}\sqrt{2}$ | D. | $\frac{3}{2}\sqrt{2}$ |
15.已知点C(3,4),抛物线y2=8x的准线为L,设抛物线上任意一点P到直线L的距离为m,则m+|PC|的最小值为( )
| A. | 5 | B. | $\sqrt{41}$ | C. | $\sqrt{41}$-2 | D. | 4 |
13.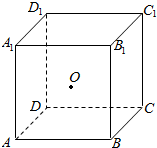 正方体ABCD-A1B1C1D1边长为2,O为正方体的中心,动点P在正方体底面ABCD内运动(包括边界),若AO⊥OP,则点P的轨迹为( )
正方体ABCD-A1B1C1D1边长为2,O为正方体的中心,动点P在正方体底面ABCD内运动(包括边界),若AO⊥OP,则点P的轨迹为( )
 正方体ABCD-A1B1C1D1边长为2,O为正方体的中心,动点P在正方体底面ABCD内运动(包括边界),若AO⊥OP,则点P的轨迹为( )
正方体ABCD-A1B1C1D1边长为2,O为正方体的中心,动点P在正方体底面ABCD内运动(包括边界),若AO⊥OP,则点P的轨迹为( )| A. | 椭圆的一部分 | B. | 线段 | C. | 圆的部分 | D. | 抛物线的一部分 |
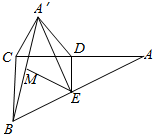 已知在△ABC中,D,E分别为AC,AB的中点,沿DE将△ADE折起,使A到A′的位置,若M是A′B的中点,求证:ME∥平面A′CD.
已知在△ABC中,D,E分别为AC,AB的中点,沿DE将△ADE折起,使A到A′的位置,若M是A′B的中点,求证:ME∥平面A′CD.