题目内容
Sn为数列bn的前n项和,且满足b1=1,
=1(n≥2).证明数列{
}成等差数列,并求数列{bn}的通项公式.
| 2bn | ||
bnSn
|
| 1 |
| Sn |
考点:等差数列的性质
专题:等差数列与等比数列
分析:由数列递推式得到
-
=
(n≥2),由此证得数列{
}成等差数列,求其通项公式后可得Sn,再由
bn=Sn-Sn-1(n≥2)求数列{bn}的通项公式.
| 1 |
| Sn |
| 1 |
| Sn-1 |
| 1 |
| 2 |
| 1 |
| Sn |
bn=Sn-Sn-1(n≥2)求数列{bn}的通项公式.
解答:
证明:由
=1(n≥2),得2bn=bnSn-Sn2(n≥2),
∴2(Sn-Sn-1)=(Sn-Sn-1)Sn-Sn2(n≥2),
即2Sn-1-2Sn=Sn•Sn-1,
∴
-
=
(n≥2).
∴数列{
}成以
为公差的等差数列,
则
=
+
(n-1)=1+
-
=
.
∴Sn=
.
当n≥2时,bn=Sn-Sn-1=
-
=-
.
当n=1时上式不成立.
∴bn=
.
| 2bn | ||
bnSn
|
∴2(Sn-Sn-1)=(Sn-Sn-1)Sn-Sn2(n≥2),
即2Sn-1-2Sn=Sn•Sn-1,
∴
| 1 |
| Sn |
| 1 |
| Sn-1 |
| 1 |
| 2 |
∴数列{
| 1 |
| Sn |
| 1 |
| 2 |
则
| 1 |
| Sn |
| 1 |
| b1 |
| 1 |
| 2 |
| n |
| 2 |
| 1 |
| 2 |
| n+1 |
| 2 |
∴Sn=
| 2 |
| n+1 |
当n≥2时,bn=Sn-Sn-1=
| 2 |
| n+1 |
| 2 |
| n |
| 2 |
| n(n+1) |
当n=1时上式不成立.
∴bn=
|
点评:本题考查了数列递推式,考查了等差关系的确定,考查了等差数列的性质,是中档题.

练习册系列答案
相关题目
已知集合A={x|x≤1},若B⊆A,则集合B可以是( )
| A、{x|x≤2} |
| B、{x|x>1} |
| C、{x|x≤0} |
| D、R |
已知直线l1:2x-y+1=0,l2:x-3y-6=0则l1到l2的角是( )
| A、45° | B、60° |
| C、120° | D、135° |
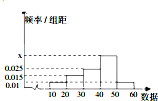 如图是一个样本数据的频率分布直方图,根据频率分布直方图,解答下列问题.
如图是一个样本数据的频率分布直方图,根据频率分布直方图,解答下列问题.