题目内容
17.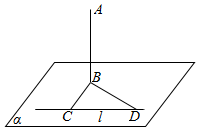 如图所示,直线AB垂直平面α于点B,直线l在平面α内,点C,D在l上,∠BCD=90°,∠CDB=45°,AB=80cm,CD=60cm.求点A到直线l的距离.
如图所示,直线AB垂直平面α于点B,直线l在平面α内,点C,D在l上,∠BCD=90°,∠CDB=45°,AB=80cm,CD=60cm.求点A到直线l的距离.
分析 连接AC,证明AC就是点A到直线l的距离.
解答  解:直线AB垂直平面α于点B,直线l在平面α内,点C,D在l上,∠BCD=90°,可得CD⊥平面ABC,
解:直线AB垂直平面α于点B,直线l在平面α内,点C,D在l上,∠BCD=90°,可得CD⊥平面ABC,
∴AC⊥CD,AC就是点A到直线l的距离
∠CDB=45°,AB=80cm,CD=60cm.
可得BC=60cm,
AC=$\sqrt{8{0}^{2}+6{0}^{2}}$=100cm.
点A到直线l的距离为100cm.
点评 本题考查空间点到直线的距离的求法,直线与平面垂直的判定定理的应用考查空间想象能力以及计算能力.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
7.等比数列{an}中,Sn表示其前n项和,a3=2S2+1,a4=2S3+1,则公比q为( )
| A. | ±2 | B. | ±3 | C. | 2 | D. | 3 |
12.现有四个函数:①y=x•sinx;②y=x•cosx;③y=x•|cosx|;④y=x•2x的图象(部分)如图,则按照从左到右的顺序,图象对应的函数序号正确的一组是( )
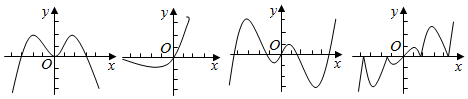
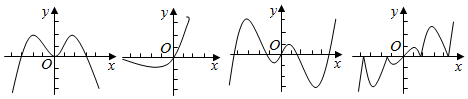
| A. | ①④③② | B. | ①④②③ | C. | ④①②③ | D. | ③④②① |
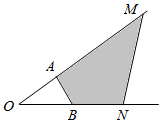 如图,A、B分别是射线OM、ON上的点,给出下列以O为起点的向量:①$\overrightarrow{OA}+2\overrightarrow{OB}$;②$\frac{1}{2}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$;③$\frac{3}{4}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$;④$\frac{3}{4}\overrightarrow{OA}$+$\frac{1}{3}\overrightarrow{OB}$;⑤$\frac{3}{4}\overrightarrow{OA}+\overrightarrow{BA}+\frac{2}{3}\overrightarrow{OB}$.其中终点落在阴影区域内的向量的序号有( )
如图,A、B分别是射线OM、ON上的点,给出下列以O为起点的向量:①$\overrightarrow{OA}+2\overrightarrow{OB}$;②$\frac{1}{2}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$;③$\frac{3}{4}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$;④$\frac{3}{4}\overrightarrow{OA}$+$\frac{1}{3}\overrightarrow{OB}$;⑤$\frac{3}{4}\overrightarrow{OA}+\overrightarrow{BA}+\frac{2}{3}\overrightarrow{OB}$.其中终点落在阴影区域内的向量的序号有( )