题目内容
5.在锐角△ABC中,已知$∠B=\frac{π}{3},|{\overrightarrow{BC}}|=2$,则$\overrightarrow{AB}•\overrightarrow{AC}$的取值范围是(0,12).分析 以B为原点,BA所在直线为x轴建立坐标系,得到C的坐标,找出三角形为锐角三角形的A的位置,得到所求范围
解答 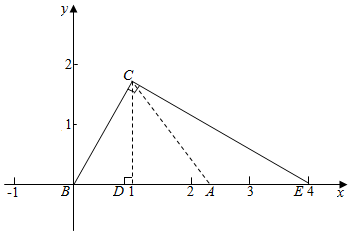 解:以B为原点,BA所在直线为x轴建立坐标系,
解:以B为原点,BA所在直线为x轴建立坐标系,
因为∠B=$\frac{π}{3}$,|$\overrightarrow{BC}$|=2,所以C(1,$\sqrt{3}$),设A(x,0)
因为△ABC是锐角三角形,所以A+C=120°,
∴30°<A<90°,即A在如图的线段DE上(不与D,E重合),所以1<x<4,
则$\overrightarrow{AB}•\overrightarrow{AC}$=x2-x=(x-$\frac{1}{2}$)2-$\frac{1}{4}$,所以则$\overrightarrow{AB}•\overrightarrow{AC}$的范围为(0,12).
故答案为:(0,12).
点评 本题考查了向量的几何意义以及利用坐标法求数量积范围,属于中档题.

练习册系列答案
相关题目
13.已知等比数列{an}满足a1+a3+a7=22,a5+a7+a11=88,则a7+a9+a13=( )
| A. | 121 | B. | 154 | C. | 176 | D. | 352 |
20.小明试图将一箱中的24瓶啤酒全部取出,每次小明在取出啤酒时只能取出三瓶或四瓶啤酒,那么小明取出啤酒的方式共有 种.( )
| A. | 18 | B. | 27 | C. | 37 | D. | 212 |
15.已知函数f(x)=2sin(x+$\frac{π}{3}$),设a=f($\frac{π}{7}$),b=f($\frac{π}{6}$),c=f($\frac{π}{3}$),则a,b,c的大小关系是( )
| A. | a<b<c | B. | c<a<b | C. | b<a<c | D. | b<c<a |
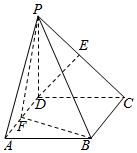 四棱锥P-ABCD中,四边形ABCD为正方形,PD⊥平面ABCD,PD=DA=2,F,E分别为AD、PC的中点.
四棱锥P-ABCD中,四边形ABCD为正方形,PD⊥平面ABCD,PD=DA=2,F,E分别为AD、PC的中点.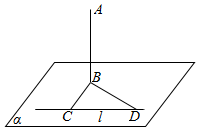 如图所示,直线AB垂直平面α于点B,直线l在平面α内,点C,D在l上,∠BCD=90°,∠CDB=45°,AB=80cm,CD=60cm.求点A到直线l的距离.
如图所示,直线AB垂直平面α于点B,直线l在平面α内,点C,D在l上,∠BCD=90°,∠CDB=45°,AB=80cm,CD=60cm.求点A到直线l的距离.