题目内容
7.写出如图阴影部分的角的集合为{α|-150°+k•360°≤α≤150°+k•360°,k∈Z}.
分析 先由图象写出角在0°~360°间的取值范围,再由终边相同的角的概念写出角的集合.
解答 解:在0°~360°内,终边落在阴影部分的角为0°≤α≤150°或210°≤α<360°,
∴终边落在阴影部分的角的集合为:
{α|0°+k•360°≤α≤150°+k•360°或210°+k•360°≤α<360°+k•360°,k∈Z}
={α|-150°+k•360°≤α≤150°+k•360°,k∈Z}.
故答案为:{α|-150°+k•360°≤α≤150°+k•360°,k∈Z}.
点评 本题考查了角的集合应用问题,解题时应注意终边相同的角的概念的合理运用,是基础题.

练习册系列答案
相关题目
15.已知函数f(x)=2sin(x+$\frac{π}{3}$),设a=f($\frac{π}{7}$),b=f($\frac{π}{6}$),c=f($\frac{π}{3}$),则a,b,c的大小关系是( )
| A. | a<b<c | B. | c<a<b | C. | b<a<c | D. | b<c<a |
2.若10件产品中有2件次品,现从中任取3件,则至少有一件是次品的取法共有( )
| A. | 72种 | B. | 64种 | C. | 36种 | D. | 16种 |
12.函数f(x)=2sin(2x+$\frac{π}{6}$)的图象( )
| A. | 关于直线x=$\frac{π}{6}$对称 | B. | 关于直线x=-$\frac{π}{12}$对称 | ||
| C. | 关于点($\frac{2π}{3}$,0)对称 | D. | 关于点(π,0)对称 |
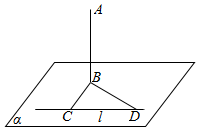 如图所示,直线AB垂直平面α于点B,直线l在平面α内,点C,D在l上,∠BCD=90°,∠CDB=45°,AB=80cm,CD=60cm.求点A到直线l的距离.
如图所示,直线AB垂直平面α于点B,直线l在平面α内,点C,D在l上,∠BCD=90°,∠CDB=45°,AB=80cm,CD=60cm.求点A到直线l的距离.