题目内容
6.已知正项数列{an}中a1=1,且${a}_{n}^{2}$•an+1+(Sn-Sn-1)2-an•an+1=0,则an=$\frac{1}{n}$.分析 由题意可得$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=1,继而得到数列{$\frac{1}{{a}_{n}}$}是以1为首项,以公差为1的等差数列,即可求出通项公式.
解答 解:∵${a}_{n}^{2}$•an+1-(Sn-Sn-1)2+an•an+1=0,
∴${a}_{n}^{2}$•an+1-an2+an•an+1=0,
∵正项数列{an},
∴an•an+1-an+an+1=0,
∴$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=1,
∵a1=1,
∴$\frac{1}{{a}_{1}}$=1,
∴数列{$\frac{1}{{a}_{n}}$}是以1为首项,以公差为1的等差数列,
∴$\frac{1}{{a}_{n}}$=1+(n-1)=n,
∴an=$\frac{1}{n}$
故答案为:$\frac{1}{n}$
点评 本题考查数列递推式,通项公式的关系,等差数列的定义的应用,考查计算能力,是中档题.

练习册系列答案
相关题目
15.已知函数f(x)=2sin(x+$\frac{π}{3}$),设a=f($\frac{π}{7}$),b=f($\frac{π}{6}$),c=f($\frac{π}{3}$),则a,b,c的大小关系是( )
| A. | a<b<c | B. | c<a<b | C. | b<a<c | D. | b<c<a |
12.函数f(x)=2sin(2x+$\frac{π}{6}$)的图象( )
| A. | 关于直线x=$\frac{π}{6}$对称 | B. | 关于直线x=-$\frac{π}{12}$对称 | ||
| C. | 关于点($\frac{2π}{3}$,0)对称 | D. | 关于点(π,0)对称 |
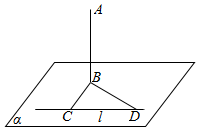 如图所示,直线AB垂直平面α于点B,直线l在平面α内,点C,D在l上,∠BCD=90°,∠CDB=45°,AB=80cm,CD=60cm.求点A到直线l的距离.
如图所示,直线AB垂直平面α于点B,直线l在平面α内,点C,D在l上,∠BCD=90°,∠CDB=45°,AB=80cm,CD=60cm.求点A到直线l的距离.