题目内容
14.已知等差数列{an}的公差为1,若a1,a3,a4成等比数列,则a2=( )| A. | $\frac{1}{2}$ | B. | -4 | C. | -6 | D. | -3 |
分析 由已知结合等差数列的性质列式求出首项,进一步得到a2 .
解答 解:由题意,a3=a1+2,a4=a1+3,
∵a1,a3,a4成等比数列,
∴${{a}_{3}}^{2}={a}_{1}{a}_{4}$,即$({a}_{1}+2)^{2}={a}_{1}({a}_{1}+3)$,解得a1=-4.
∴a2=a1+1=-3.
故选:D.
点评 本题考查等差数列的通项公式,考查了等差数列的性质,是基础的计算题.

练习册系列答案
相关题目
4.一圆的面积以10πcm2/s速度增加,那么当圆半径r=20cm时,其半径r的增加速率u为( )
| A. | $\frac{1}{2}$cm/s | B. | $\frac{1}{3}$cm/s | C. | $\frac{1}{4}$cm/s | D. | $\frac{1}{5}$cm/s |
2.在下列函数中,在定义域上是单调的奇函数的为( )
| A. | y=1 | B. | y=x-1 | C. | y=x+1 | D. | y=x3 |
9.设集合A={x|x2+3x-4>0},集合B={x|-2<x≤3},且M=A∩B,则有( )
| A. | 1∈M | B. | 0∈M | C. | 1∈M | D. | 2∈M |
6.一块边长为6cm的正方形铁皮按如图(1)所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正三棱锥形容器,将该容器按如图(2)放置,若其正视图为等腰直角三角形(如图(3)),则该容器的体积为( )
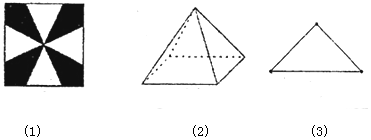

| A. | $12\sqrt{6}c{m^3}$ | B. | $4\sqrt{6}c{m^3}$ | C. | $27\sqrt{2}c{m^3}$ | D. | $9\sqrt{2}c{m^3}$ |