题目内容
6.一块边长为6cm的正方形铁皮按如图(1)所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正三棱锥形容器,将该容器按如图(2)放置,若其正视图为等腰直角三角形(如图(3)),则该容器的体积为( )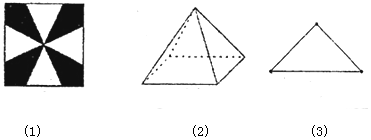
| A. | $12\sqrt{6}c{m^3}$ | B. | $4\sqrt{6}c{m^3}$ | C. | $27\sqrt{2}c{m^3}$ | D. | $9\sqrt{2}c{m^3}$ |
分析 推导出PM+PN=6,且PM=PN,MN=3$\sqrt{2}$,PM=3,设MN中点为O,则PO⊥平面ABCD,由此能求出该容器的体积.
解答 解:如图(2),△PMN是该四棱锥的正视图,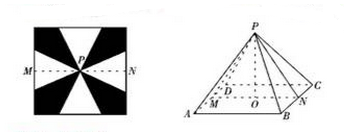
由图(1)知:PM+PN=6,且PM=PN,
由△PMN为等腰直角三角形,知MN=3$\sqrt{2}$,PM=3,
设MN中点为O,则PO⊥平面ABCD,∴PO=$\frac{1}{2}MN=\frac{3\sqrt{2}}{2}$,
∴该容器的体积为${V}_{P-ABCD}=\frac{1}{3}×(3\sqrt{2})^{2}×\frac{3\sqrt{2}}{2}$=$\frac{1}{3}×18×\frac{3\sqrt{2}}{2}$=9$\sqrt{2}$.
故选:D.
点评 解决本类题目的关键是准确理解几何体的定义,真正把握几何体的结构特征,根据条件构建几何模型,在几何模型中进行判断.

练习册系列答案
相关题目
16.三棱柱ABC-A1B1C1的侧棱与底面垂直,且所有棱长均相等,M为A1C1的中点,则直线CM和直线A1B所成角的余弦值为( )
| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{10}}}{4}$ | C. | $\frac{{\sqrt{15}}}{5}$ | D. | $\frac{9}{10}$ |
14.已知等差数列{an}的公差为1,若a1,a3,a4成等比数列,则a2=( )
| A. | $\frac{1}{2}$ | B. | -4 | C. | -6 | D. | -3 |
11.直线$y=\sqrt{3}x+1$的倾斜角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
18.已知函数y=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则ω,φ的值分别是( )


| A. | $\frac{1}{2}$,$\frac{π}{6}$ | B. | 1,$\frac{π}{6}$ | C. | 1,$\frac{π}{3}$ | D. | $\frac{1}{2}$,$\frac{π}{3}$ |
15.若方程为$\frac{x^2}{m+1}-\frac{y^2}{m-3}$=1表示双曲线,则实数m满足( )
| A. | m>3或m<-1 | B. | m≠-1且m≠3 | C. | -1<m<3 | D. | m<-1 |
16.已知实数满足a>b>c,且a+b+c=0,则下列不等式中正确的是( )
| A. | ab<ac | B. | ac<bc | C. | a|b|>c|b| | D. | a2>b2>c2 |