题目内容
20.函数f(x)=xex-x-2的零点的个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 求出函数的导数,得到函数f(x)的单调区间,从而求出函数的零点个数即可.
解答 解:f′(x)=(x+1)ex-1,
f″(x)=(x+2)ex,
令f″(x)>0,解得:x>-2,
令f″(x)<0,解得:x<-2,
故f′(x)在(-∞,-2)递减,在(-2,+∞)递增,
故f′(x)min=f′(-2)=-$\frac{1}{{e}^{2}}$-1<0,
而f′(0)=0,x→-∞时,f′(x)→-∞,
故x<0时,f′(x)<0,f(x)递减,
x>0时,f′(x)>0,f(x)递增,
故f(x)的最小值是f(0)=-2,
故函数f(x)的零点个数是2个,
故选:C.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数的零点问题,是一道中档题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
11.下列语句为命题的是( )
| A. | lg100=2 | B. | 20172017是一个大数 | ||
| C. | 三角函数的图象真漂亮! | D. | 指数函数是递增函数吗? |
9.某几何体的三视图如图,则该几何体的体积是( )
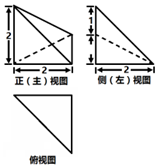

| A. | 4 | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | 2 |
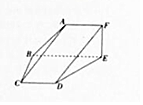 如图,平面ABEF⊥平面CBED,四边形ABEF为直角三角形,∠AFE=∠FEB=90°,四边形CBED为等腰梯形,CD∥BE,且BE=2AF=2CD=2BC=2EF=4.
如图,平面ABEF⊥平面CBED,四边形ABEF为直角三角形,∠AFE=∠FEB=90°,四边形CBED为等腰梯形,CD∥BE,且BE=2AF=2CD=2BC=2EF=4.