题目内容
1.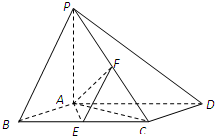 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
(1)证明:异面直线AE与PD所的角;
(2)若PD与平面ABCD所成角为45°,求二面角E-AF-C的余弦值.
分析 (1)推导出AE⊥BC,AE⊥AD,PA⊥AE,从而AE⊥平面PAD,由此能证明AE⊥PD.
(2)法一(几何法):设AB=2,过E作EO⊥AC于O,则EO⊥平面PAC,过O作OS⊥AF于S,连接ES,则∠ESO为二面角E-AF-C的平面角,由此能求出二面角E-AF-C的余弦值.
法二(向量法):设AB=2,由AE,AD,AP两两垂直,以A为坐标原点,建立空间直角坐标系,利用向量法能求出二面角E-AF-C的余弦值.
解答 证明:(1)由四边形ABCD为菱形,∠ABC=60°,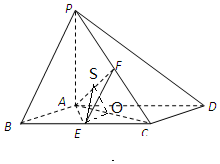
可得△ABC为正三角形.因为E为BC的中点,所以AE⊥BC.
又BC∥AD,因此AE⊥AD.
因为PA⊥平面ABCD,AE?平面ABCD,所以PA⊥AE.
而PA?平面PAD,AD?平面PAD,且PA∩AD=A,
所以AE⊥平面PAD.又PD?平面PAD,
所以AE⊥PD.…(6分)
解:(2)因为PA⊥平面ABCD,所以PD与底面ABCD所成的角为∠PDA,
因为∠PDA=45°,所以PA=AD.…(9分)
解法一:设AB=2,因为PA⊥平面ABCD,PA?平面PAC,
所以平面PAC⊥平面ABCD.过E作EO⊥AC于O,则EO⊥平面PAC,
过O作OS⊥AF于S,连接ES,则∠ESO为二面角E-AF-C的平面角,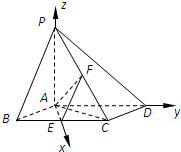
在Rt△AOE中,EO=AEsin30°=$\frac{\sqrt{3}}{2}$,AO=AEcos30°=$\frac{3}{2}$,
又F是PC的中点,在Rt△ASO中,$SO=AO•sin{45°}=\frac{{3\sqrt{2}}}{4}$,
又SE=$\sqrt{E{O}^{2}+S{O}^{2}}$=$\sqrt{\frac{3}{4}+\frac{9}{8}}$=$\frac{\sqrt{30}}{4}$,
在Rt△ESO中,cos∠ESO=$\frac{SO}{SE}=\frac{\frac{3\sqrt{2}}{4}}{\frac{\sqrt{30}}{4}}$=$\frac{\sqrt{15}}{5}$,
即所求二面角的余弦值为$\frac{\sqrt{15}}{5}$.…(12分)
解法二:设AB=2,由(Ⅰ)知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,
又E,F分别为BC,PC的中点,
所以A(0,0,0),B($\sqrt{3},-1,0$),C($\sqrt{3},1,0$),D(0,2,0),P(0,0,2),
E($\sqrt{3},0,0$),F($\frac{\sqrt{3}}{2},\frac{1}{2},1$),
所以$\overrightarrow{AE}=(\sqrt{3},0,0),\overrightarrow{AF}=({\frac{{\sqrt{3}}}{2},\frac{1}{2},1})$.
设平面AEF的一法向量为m=(x1,y1,z1),
则$\left\{\begin{array}{l}m•\overrightarrow{AE}=0\\ m•\overrightarrow{AF}=0\end{array}\right.$因此$\left\{\begin{array}{l}\sqrt{3}{x_1}=0\\ \frac{{\sqrt{3}}}{2}{x_1}+\frac{1}{2}{y_1}+{z_1}=0\end{array}\right.$,
取z1=-1,则m=(0,2,-1),因为BD⊥AC,BD⊥PA,PA∩AC=A,
所以BD⊥平面AFC,故$\overrightarrow{BD}$为平面AFC的一个法向量.
又$\overrightarrow{BD}$=(-$\sqrt{3},3,0$),所以cos<$\overrightarrow{m},\overrightarrow{BD}$>=$\frac{\overrightarrow{m}•\overrightarrow{BD}}{|\overrightarrow{m}|•|\overrightarrow{BD}|}$=$\frac{2×3}{\sqrt{5}×\sqrt{12}}$=$\frac{\sqrt{15}}{5}$.
因为二面角E-AF-C为锐角,所以所求二面角的余弦值为$\frac{\sqrt{15}}{5}$.…(12分)
点评 本题考查线线垂直的证明,考查二面角的余弦值的求法,考查推理论证能力、运算求解能力、空间想象能力,考查等价转化思想、数形结合思想,是中档题.

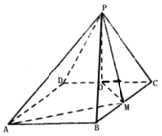 如图,四边形ABCD为矩形,平面PCD⊥平面ABCD,且PC=PD=CD=2,BC=2$\sqrt{2}$,O,M分别为CD,BC的中点,则异面直线OM与PD所成角的余弦值为( )
如图,四边形ABCD为矩形,平面PCD⊥平面ABCD,且PC=PD=CD=2,BC=2$\sqrt{2}$,O,M分别为CD,BC的中点,则异面直线OM与PD所成角的余弦值为( )| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{3}}{6}$ | D. | $\frac{\sqrt{3}}{3}$ |
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
| A. | 30 | B. | 25 | C. | 20 | D. | 12 |
| 日期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
| 平均气温x(℃) | 9 | 10 | 12 | 11 | 8 |
| 销量y(杯) | 23 | 25 | 30 | 26 | 21 |
(Ⅱ)请根据所给五组书记,求出y关于x的线性回归方程式$\widehaty=\widehatbx+\widehata$.
(Ⅲ)根据(Ⅱ)所得的线性回归方程,若天气预报1月16号的白天平均气温为7(℃),请预测该奶茶店这种饮料的销量.
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x)