题目内容
关于x的一元二次方程x2+2tx+|a+2|+|a-1|=0对任意a∈R无实根，求实数t的取值范围．
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：由题意可得△＜0，即t2＜|a+2|+|a-1|对a∈R恒成立，利用绝对值三角不等式求得（|a+2|+|a-1|）min=3，可得 t2＜3，由此求得实数t的取值范围．
解答：
解：∵关于x的一元二次方程x2+2tx+|a+2|+|a-1|=0对任意a∈R无实根，
∴△=4t2-4（|a+2|+|a-1|）＜0，即t2＜|a+2|+|a-1|对a∈R恒成立，（2分）
而|a+2|+|a-1|≥|（a+2）-（a-1）|=3，（4分）
当且仅当（a+2）（a-1）≤0，即-2≤a≤1时等号成立，∴（|a+2|+|a-1|）min=3，（6分）
∴t2＜3，求得-
＜t＜
，∴实数t的取值范围为（-
，
）．
∴△=4t2-4（|a+2|+|a-1|）＜0，即t2＜|a+2|+|a-1|对a∈R恒成立，（2分）
而|a+2|+|a-1|≥|（a+2）-（a-1）|=3，（4分）
当且仅当（a+2）（a-1）≤0，即-2≤a≤1时等号成立，∴（|a+2|+|a-1|）min=3，（6分）
∴t2＜3，求得-
| 3 |
| 3 |
| 3 |
| 3 |
点评：本小题主要考查绝对不等式、绝对值三角不等式，不等式证明等基础知识，考查推理论证能力，考查化归与转化思想，属于基础题．
练习册系列答案
相关题目
为了得到函数y=sin（3x+1），x∈R的图象，只需将函数y=sin3x，x∈R的图象（ ）
| A、向左平移1个的单位长度 | ||
| B、向右平移1个的单位长度 | ||
C、向左平移
| ||
D、向右平移
|
已知函数f(x)=
x2-ax+lnx在（0，+∞）上是增函数，则a的取值范围是（ ）
| 1 |
| 2 |
| A、（-∞，2） |
| B、（-∞，2] |
| C、（-2，2） |
| D、[-2，2] |
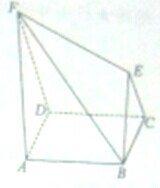在如图所示的几何体中，四边形ABCD为正方形，DF∥CE，DF⊥DC，且DF=2AD=2CE，AF=