圆的直径AB上有两点C.D.且|AB|=10.|AC|=|BD|=4.P为圆上一点.求|PC|+|PD|的最大值．题目和参考答案——青夏教育精英家教网—

题目内容

圆的直径AB上有两点C，D，且|AB|=10，|AC|=|BD|=4，P为圆上一点，求|PC|+|PD|的最大值．

考点：圆的参数方程

专题：直线与圆,坐标系和参数方程

分析：如图建立平面直角坐标系，根据|AB|的长，表示出圆的参数方程，由|AC|=|BD|=4，求出C与D坐标，根据P在圆上，表示出P坐标，利用两点间的距离公式表示出|PC|+|PD|，利用余弦函数的值域即可求出最大值．

解答：

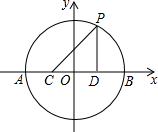解：如图建立平面直角坐标系，
∵|AB|=10，
∴圆的参数方程为

x=5cosθ

y=5sinθ

（θ为参数），
∵|AC|=|BD|=4，
∴C（-1，0），D（1，0），
∵点P在圆上，
∴P坐标为（5cosθ，5sinθ），
∴（|PC|+|PD|）²=（

26+10cosθ

26-10cosθ

）²=52+2

262-100cos2θ

，
当cosθ=0时，（|PC|+|PD|）²_max=104，
则（|PC|+|PD|）_max=2

．

点评：此题考查了圆的参数方程，两点间的距离公式，余弦函数的值域，表示出圆的参数方程是解本题的关键．

练习册系列答案

关于x的一元二次方程x²+2tx+|a+2|+|a-1|=0对任意a∈R无实根，求实数t的取值范围．

=1，（a＞0，b＞0）上，另一点在直线l上．
（1）求双曲线方程；
（2）设直线l的斜率存在且为k，它与双曲线的同一支分别交于两点E、F，M、N分别为双曲线的左、右顶点，求满足条件

•

=32的k值．

设函数f（x）=lnx+e^x，g（x）=e^x+

x²-ax（a∈R）（e=2.71828…是自然对数的底数）
（1）当a=

，设F（x）=f（x）-g（x），求F（x）的单调区间；
（2）定义：若函数φ（x）在定义域为[m，n]（m＜n）上的值域为[m，n]，则称区间[m，n]为函数φ（x）的“同域区间”，在（1）的条件下，证明：函数F（x）在区间（0，2）内存在“同域区间”；
（3）当a＞1时，对于区间（2，3）内任意两个不相等的实数x₁，x₂都有|f（x₁）-f（x₂）|＞|g（x₁）-g（x₂）|成立，求a的取值范围．

在一个盒子中装有6枝圆珠笔，其中3枝黑色，2枝蓝色，1枝红色，从中任取3枝．
（1）该实验的基本事件共有多少个？若将3枝黑色圆珠笔编号为A、B、C，2枝蓝色圆珠笔编号为d，e，1枝红色圆珠笔编号为x，用{a，b，c}表示基本事件，试列举出该实验的所有基本事件；
（2）求恰有一枝黑色的概率；
（3）求至少1枝蓝色的概率．

已知函数f（x）=ae^x-1（e为自然对数的底数，a为常数）的图象与直线y=x相切．
（Ⅰ）求a的值，并求函数y=f（x）-x的值域；
（Ⅱ）设g（x）=lnx+1，证明：当x＞0时，f（x）＞g（x）．

已知函数f（x）=（x+1）e^-x（e为自然对数的底数）．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）设函数φ（x）=xf（x）+tf′（x）+e^-x，存在x₁，x₂∈[0，1]，使得成立2φ（x₁）＜φ（x₂）成立，求实数t的取值范围．

试题分类