题目内容
已知两条直线l1:x+my+
=0,l2:(m-2)x+15y+2m=0,当m为何值时,l1与l2:
(1)平行;
(2)相交;
(3)垂直;
(4)重合.
| 6 |
| 5 |
(1)平行;
(2)相交;
(3)垂直;
(4)重合.
考点:直线的一般式方程
专题:直线与圆
分析:对于直线的一般式方程,当直线方程中一次项系数之比相等,但不等于常数项之比时,两条直线平行;当当直线方程中一次项系数之比不相等时,两条直线相交;当直线方程中一次项系数对应项之积的和等于零时,两条直线垂直;当直线方程中一次项系数之比相等,且还等于等于常数项之比时,两条直线重合.
解答:
解:(1)当
=
≠
,即m=5时,l1与l2平行.
(2)当
≠
,即m≠5 且m≠-3时,l1与l2相交.
(3)当1×(m-2)+m×15=0时,即 m=
时,l1与l2相垂直.
(4)当
=
=
,即m=-3时,l1与l2重合.
| 1 |
| m-2 |
| m |
| 15 |
| ||
| 2m |
(2)当
| 1 |
| m-2 |
| m |
| 15 |
(3)当1×(m-2)+m×15=0时,即 m=
| 1 |
| 8 |
(4)当
| 1 |
| m-2 |
| m |
| 15 |
| ||
| 2m |
点评:本题主要考查两条直线平行、相交、垂直、重合条件,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=f(x)是定义在R上的可导函数,则x=x0为函数y=f(x)的极值点是f′(x0)=0的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
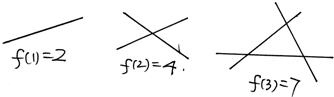 对于问题:“两两相交且任三条不共点的n条直线把平面分为f(n)部分”,我们由归纳推理得到f(10)=( )
对于问题:“两两相交且任三条不共点的n条直线把平面分为f(n)部分”,我们由归纳推理得到f(10)=( )| A、54 | B、55 | C、56 | D、57 |
已知双曲线
-
=1(a>0,b>0),右焦点F到渐近线的距离小于等于a,则该双曲线离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(
| ||
B、[
| ||
C、(1,
| ||
D、(1,
|
在△ABC中,若a=7,b=8,cosC=
,则c=( )
| 13 |
| 14 |
| A、1 | B、2 | C、3 | D、4 |
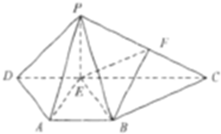 如图,在四棱维P-ABCD中,侧面PCD⊥底面ABCD.四边形ABCD是等腰梯形.AB∥CD.∠ADC=∠PDC=
如图,在四棱维P-ABCD中,侧面PCD⊥底面ABCD.四边形ABCD是等腰梯形.AB∥CD.∠ADC=∠PDC= 将形如
将形如