题目内容
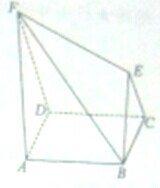在如图所示的几何体中，四边形ABCD为正方形，DF∥CE，DF⊥DC，且DF=2AD=2CE，AF=| 3 |
（Ⅰ）求证：BE∥平面ADF；
（Ⅱ）求证：AF⊥平面ABCD．
考点：直线与平面垂直的判定,直线与平面平行的判定
专题：空间位置关系与距离
分析：（Ⅰ）取DF的中点G，连接GE，AG，先通过证明四边形ABEG为平行四边形，推断出BE∥AG，进而根据线面平行的判定定理证明出BE∥平面ADF．
（Ⅱ）利用线面垂直的判定定理证明出CD⊥平面ADF，进而可证明出CD⊥FA，然后通过勾股定理证明出DF⊥AD，最后利用线面平行的判定定理证明出AF⊥平面ABCD．
（Ⅱ）利用线面垂直的判定定理证明出CD⊥平面ADF，进而可证明出CD⊥FA，然后通过勾股定理证明出DF⊥AD，最后利用线面平行的判定定理证明出AF⊥平面ABCD．
解答：
证明：（Ⅰ）取DF的中点G，连接GE，AG，
∵CE=
DF，DG=
DF，DF∥CE，
∴CE∥DG且CE=DG，
∴四边形ABEG为平行四边形，
∴BE∥AG，
∵AG?平面ADF，BE?平面ADF，
∴BE∥平面ADF．
（Ⅱ）∵ABCD为正方形，
∴AD⊥CD，
∵DF⊥DC，DF?平面ADF，AD?平面ADF，AD∩DF=D，
∴CD⊥平面ADF，
∵FA?平面ADF，
∴CD⊥FA，
∵AF=
AD，DF=2AD
∴DF2=AF2+AD2，
∴DF⊥AD，
∵AD?平面ABCD，CD?平面ABCD，CD∩AD=D，
∴AF⊥平面ABCD．
证明：（Ⅰ）取DF的中点G，连接GE，AG，∵CE=
| 1 |
| 2 |
| 1 |
| 2 |
∴CE∥DG且CE=DG，
∴四边形ABEG为平行四边形，
∴BE∥AG，
∵AG?平面ADF，BE?平面ADF，
∴BE∥平面ADF．
（Ⅱ）∵ABCD为正方形，
∴AD⊥CD，
∵DF⊥DC，DF?平面ADF，AD?平面ADF，AD∩DF=D，
∴CD⊥平面ADF，
∵FA?平面ADF，
∴CD⊥FA，
∵AF=
| 3 |
∴DF2=AF2+AD2，
∴DF⊥AD，
∵AD?平面ABCD，CD?平面ABCD，CD∩AD=D，
∴AF⊥平面ABCD．
点评：本题主要考查了线面垂直和线面平行的判定定理的应用．考查了学生三维观察能力和推理能力．
练习册系列答案
相关题目
对任意复数z=x+yi（x，y∈R），i为虚数单位，则下列结论正确的是（ ）
| A、|z|≤|x|+|y| | ||
B、|z-
| ||
| C、z2=x2+y2 | ||
D、|z-
|
已知双曲线
-
=1（a＞0，b＞0），右焦点F到渐近线的距离小于等于a，则该双曲线离心率的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、（
| ||
B、[
| ||
C、（1，
| ||
D、（1，
|
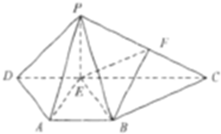如图，在四棱维P-ABCD中，侧面PCD⊥底面ABCD．四边形ABCD是等腰梯形．AB∥CD．∠ADC=∠PDC=