题目内容
已知函数f(x)=
x2-ax+lnx在(0,+∞)上是增函数,则a的取值范围是( )
| 1 |
| 2 |
| A、(-∞,2) |
| B、(-∞,2] |
| C、(-2,2) |
| D、[-2,2] |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:求出导函数,据导函数的符号与函数单调性的关系,令导函数大于等于0恒成立,分离出a,利用基本不等式求出函数的最小值,令a小于等于最小值即可得到a的范围.
解答:
解:(1)f′(x)=x-a+
,
∵f(x)在(0,1)上是增函数,
∴x+
-a≥0在(0,1)上恒成立,
即a≤x+
恒成立,
∴只需a≤(x+
)min即可.
∴x+
≥2(当且仅当x=1时取等号),
∴a≤2.
故选:B.
| 1 |
| x |
∵f(x)在(0,1)上是增函数,
∴x+
| 1 |
| x |
即a≤x+
| 1 |
| x |
∴只需a≤(x+
| 1 |
| x |
∴x+
| 1 |
| x |
∴a≤2.
故选:B.
点评:解决函数的单调性已知求参数的范围问题,常求出导函数,令导函数大于等于(或小于等于)0恒成立.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
已知函数f(x)=x2•cos(xπ),若an=f(n)+f(n+1),则
ai=( )
| 2014 |
 |
| i=1 |
| A、-2015 | B、-2014 |
| C、2014 | D、2015 |
对任意复数z=x+yi(x,y∈R),i为虚数单位,则下列结论正确的是( )
| A、|z|≤|x|+|y| | ||
B、|z-
| ||
| C、z2=x2+y2 | ||
D、|z-
|
正项等比数列{an}中,如果a1+a4+a7=3,a3+a6+a9=27,则数列{an}前9项的和为( )
| A、39 | B、21 | C、49 | D、31 |
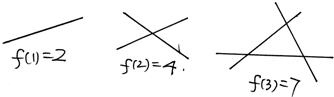 对于问题:“两两相交且任三条不共点的n条直线把平面分为f(n)部分”,我们由归纳推理得到f(10)=( )
对于问题:“两两相交且任三条不共点的n条直线把平面分为f(n)部分”,我们由归纳推理得到f(10)=( )| A、54 | B、55 | C、56 | D、57 |
已知
,则z=x-2y的最小值为( )
|
| A、2 | B、0 | C、-2 | D、-4 |
已知双曲线
-
=1(a>0,b>0),右焦点F到渐近线的距离小于等于a,则该双曲线离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(
| ||
B、[
| ||
C、(1,
| ||
D、(1,
|