题目内容
7.为了研究钟表与三角函数的关系,以9点与3点所在直线为x轴,以6点与12点为y轴,设秒针针尖指向位置P(x,y),若初始位置为P0($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),秒针从P0(注此时t=0)开始沿顺时针方向走动,则点P的纵坐标y与时间t(秒)的函数关系为( )| A. | y=sin($\frac{π}{30}$t+$\frac{π}{3}$) | B. | y=sin($\frac{π}{30}$t-$\frac{π}{3}$) | C. | y=sin(-$\frac{π}{30}$t+$\frac{π}{3}$) | D. | y=sin(-$\frac{π}{30}$t-$\frac{π}{3}$) |
分析 求出转速ω 的值,再求出经过时间t,秒针与x正半轴的夹角以及秒针的长度为|OP|,即可求得点P的纵坐标y与时间t的函数关系.
解答 解:以9点与3点所在直线为x轴,以6点与12点为y轴,设秒针针尖指向位置P(x,y),
若初始位置为P0($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),秒针从P0(注此时t=0)开始沿顺时针方向走动,
由于秒针每60秒顺时针转一周,故转速ω=-$\frac{2π}{60}$=-$\frac{π}{30}$,
由于初始位置为P0($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),故经过时间t,秒针与x正半轴的夹角为-$\frac{π}{30}$t+$\frac{π}{3}$,
再由秒针的长度为|OP|=1,可得点P的纵坐标y与时间t的函数关系为y=sin(-$\frac{π}{30}$ t+$\frac{π}{3}$),
故选:C.
点评 本题主要考查由函数y=Asin(ωx+∅)的部分图象求函数的解析式,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知数列{an}中,a1=1,若an+1=3an+2(n∈N*),则数列{an}的通项公式an=( )
| A. | 2×3n-1 | B. | 2×3n-1-1 | C. | 2×3n-1+1 | D. | 3×2n-1-2 |
12.已知函数f(x)=3x2+2ax-a2,其中a∈(0,3],f(x)≤0对任意的x∈[-1,1]都成立,在1和a两数间插入2015个数,使之与1,a构成等比数列,设插入的这2015个数的乘积为T,则T=( )
| A. | 22015 | B. | 32015 | C. | ${3}^{\frac{2015}{2}}$ | D. | ${2}^{\frac{2015}{2}}$ |
17.下列函数既是奇函数又在(-1,1)上是增函数的是( )
| A. | y=cos($\frac{π}{2}$+x) | B. | y=-$\frac{2}{x}$ | C. | y=ln$\frac{2-x}{2+x}$ | D. | y=2x-2-x |
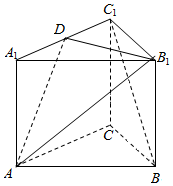 已知三棱柱ABC-A1B1C1,△ABC是正三角形,直线AA1⊥平面A1B1C1,D是棱A1C1的中点.
已知三棱柱ABC-A1B1C1,△ABC是正三角形,直线AA1⊥平面A1B1C1,D是棱A1C1的中点.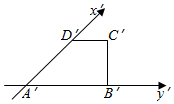 如图,四边形A′B′C′D′是直角梯形,它是四边形ABCD水平放置时的直观图,下底A′B′=20,上底C′D′=10,垂直于底的腰B′C′=10,求B′C′在原平面图形ABCD中的对应线段BC的长度.
如图,四边形A′B′C′D′是直角梯形,它是四边形ABCD水平放置时的直观图,下底A′B′=20,上底C′D′=10,垂直于底的腰B′C′=10,求B′C′在原平面图形ABCD中的对应线段BC的长度.