题目内容
15.已知数列{an}中,a1=1,若an+1=3an+2(n∈N*),则数列{an}的通项公式an=( )| A. | 2×3n-1 | B. | 2×3n-1-1 | C. | 2×3n-1+1 | D. | 3×2n-1-2 |
分析 由an+1=3an+2(n∈N*),变形为:an+1+1=3(an+1),利用等比数列的通项公式即可得出.
解答 解:∵an+1=3an+2(n∈N*),
变形为:an+1+1=3(an+1),
∴数列{an+1}为等比数列,公比为3,首项为2.
∴an+1=2×3n-1,.
则数列{an}的通项公式an=2×3n-1-1.
故选:B
点评 本题考查了等比数列的通项公式、递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.若实数x,y满足约束条件$\left\{\begin{array}{l}{x-y-2≤0}\\{x+2y-7≥0}\\{y-3≤0}\end{array}\right.$,则z=$\frac{y}{x+1}$的最大值为( )
| A. | $\frac{3}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{5}{14}$ |
6.复数($\frac{1+i}{1-i}$)3的模是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
7.为了研究钟表与三角函数的关系,以9点与3点所在直线为x轴,以6点与12点为y轴,设秒针针尖指向位置P(x,y),若初始位置为P0($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),秒针从P0(注此时t=0)开始沿顺时针方向走动,则点P的纵坐标y与时间t(秒)的函数关系为( )
| A. | y=sin($\frac{π}{30}$t+$\frac{π}{3}$) | B. | y=sin($\frac{π}{30}$t-$\frac{π}{3}$) | C. | y=sin(-$\frac{π}{30}$t+$\frac{π}{3}$) | D. | y=sin(-$\frac{π}{30}$t-$\frac{π}{3}$) |
4.两人掷一枚硬币,掷出正面多者为胜,但这枚硬币质地不均匀,以致出现正面的概率P1与出现反面的概率P2不相等,已知出现正面与出现反面是对立事件,设两人各掷一次成平局的概率为P,则P与0.5的大小关系是( )
| A. | P<0.5 | B. | P=0.5 | C. | P>0.5 | D. | 不确定 |
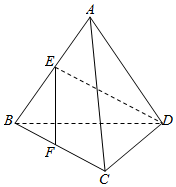 如图,已知正三角形BCD外一点A满足AB=AD,E,F分别是AB,BC的中点,且EF⊥DE,则∠BAC=$\frac{π}{2}$.
如图,已知正三角形BCD外一点A满足AB=AD,E,F分别是AB,BC的中点,且EF⊥DE,则∠BAC=$\frac{π}{2}$.