题目内容
17．
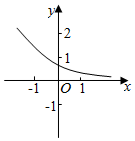函数f（x）=ax-b的图象如图，其中a，b为常数，则下列结论正确的是（ ）| A． | a＞1，b＜0 | B． | a＞1，b＞0 | C． | 0＜a＜1，b＞0 | D． | 0＜a＜1，b＜0 |
分析 应用图象的单调性，及x=0时，0＜y＜1，判断a、b的范围．
解答 解：由图象知道：f（0）=1-b＜1，∴b＞0；函数为减函数，∴0＜a＜1．
故选 C．
点评 本题考查指数函数图象及性质，考查观察图象的能力，属于基础题．
练习册系列答案
相关题目
1．若$m=tan{20^o}+tan{40^o}+\sqrt{3}tan{20^o}tan{40^o}$，则m=（ ）
| A． | $-\sqrt{3}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $-\frac{{\sqrt{3}}}{3}$ | D． | $\sqrt{3}$ |
2．将一颗质地均匀的骰子（一种各面上分别标有1、2、3、4、5、6的正方体玩具），先后抛掷3次，至少出现一次4点向上的概率是（ ）
| A． | $\frac{5}{216}$ | B． | $\frac{31}{216}$ | C． | $\frac{91}{216}$ | D． | $\frac{25}{216}$ |
设函数f（x）=|log2（x+2）|-1．
6．下列各式正确的是（ ）
| A． | $\root{6}{{{{（-3）}^2}}}=\root{3}{-3}$ | B． | $\root{4}{a^4}=a$ | C． | $\root{6}{2^2}=\root{3}{2}$ | D． | a0=1 |
7．f（x）=sin（x-α），f（x）在〔0，$\frac{π}{3}$〕上的定积分等于0，则tanα=（ ）
| A． | $\sqrt{3}$ | B． | -$\sqrt{3}$ | C． | $\frac{1}{{\sqrt{3}}}$ | D． | -$\frac{1}{{\sqrt{3}}}$ |