题目内容
2.已知矩形ABCD的边AB长为2,边AD长为$\sqrt{3}$,点E是AB边上的动点,则 $\overrightarrow{DE}$•$\overrightarrow{DC}$ 的最大值为4.分析 由题意画出图形,分别以AB,AD所在直线为x轴,y轴建立平面直角坐标系,设出E的坐标(x,0)(0≤x≤2),把 $\overrightarrow{DE}$、$\overrightarrow{DC}$ 的坐标用含有x的代数式表示,结合x的范围求得$\overrightarrow{DE}$•$\overrightarrow{DC}$ 的最大值.
解答 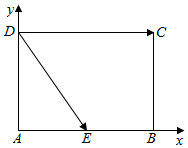 解:如图,
解:如图,
分别以AB,AD所在直线为x轴,y轴建立平面直角坐标系,
∵AB=2,AD=$\sqrt{3}$,
∴D(0,$\sqrt{3}$),C(2,$\sqrt{3}$),
设E(x,0)(0≤x≤2),
∴$\overrightarrow{DC}=(2,0)$,$\overrightarrow{DE}=(x,-\sqrt{3})$,
则$\overrightarrow{DE}•\overrightarrow{DC}$=2x,
则当x=2时,$\overrightarrow{DE}$•$\overrightarrow{DC}$ 有最大值为4.
故答案为:4.
点评 本题考查平面向量的数量积运算,考查了数量积的坐标表示,建立平面直角坐标系起到事半功倍的效果,是中档题.

练习册系列答案
相关题目
17.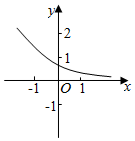 函数f(x)=ax-b的图象如图,其中a,b为常数,则下列结论正确的是( )
函数f(x)=ax-b的图象如图,其中a,b为常数,则下列结论正确的是( )
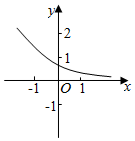 函数f(x)=ax-b的图象如图,其中a,b为常数,则下列结论正确的是( )
函数f(x)=ax-b的图象如图,其中a,b为常数,则下列结论正确的是( )| A. | a>1,b<0 | B. | a>1,b>0 | C. | 0<a<1,b>0 | D. | 0<a<1,b<0 |
14.已知两点A(2,1),B(5,5)到直线l的距离分别为2,3,则满足条件的直线l共有( )条.
| A. | 4 | B. | 3 | C. | 2 | D. | 11 |




 如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间t(月)的关系:f(t)=at,有以下叙述:
如图所示的是某池塘中的浮萍蔓延的面积(m2)与时间t(月)的关系:f(t)=at,有以下叙述: