题目内容
1.若$m=tan{20^o}+tan{40^o}+\sqrt{3}tan{20^o}tan{40^o}$,则m=( )| A. | $-\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $-\frac{{\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
分析 由条件利用两角和的正切公式,求得m的值.
解答 解:∵$m=tan{20^o}+tan{40^o}+\sqrt{3}tan{20^o}tan{40^o}$
=tan(20°+40°)(1-tan20°tan40°)+$\sqrt{3}$tan20°tan40°
=$\sqrt{3}$(1-tan20°tan40°)+$\sqrt{3}$tan20°tan40°=$\sqrt{3}$,
故选:D.
点评 本题主要考查两角和的正切公式的应用,属于基础题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
13.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左.右焦点分别为F1、F2过点F1并且垂直于x轴的直线为l.若过原点O和F2并和直线l相切的圆的半径等于点F2到双曲线C的两条渐近线的距离之和.则双曲线C的离心率为( )
| A. | $\frac{\sqrt{7}}{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{4\sqrt{7}}{7}$ |
10.已知函数f(x)=x2+2x(x>0),f1(x)=f(x),fn+1(x)=f(fn(x)),n∈N*,则f5(x)在[1,2]上的最大值是( )
| A. | 210-1 | B. | 232-1 | C. | 310-1 | D. | 332-1 |
17.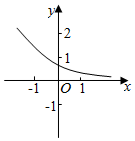 函数f(x)=ax-b的图象如图,其中a,b为常数,则下列结论正确的是( )
函数f(x)=ax-b的图象如图,其中a,b为常数,则下列结论正确的是( )
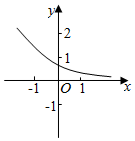 函数f(x)=ax-b的图象如图,其中a,b为常数,则下列结论正确的是( )
函数f(x)=ax-b的图象如图,其中a,b为常数,则下列结论正确的是( )| A. | a>1,b<0 | B. | a>1,b>0 | C. | 0<a<1,b>0 | D. | 0<a<1,b<0 |