题目内容
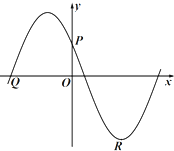 如图,点P(0,
如图,点P(0,| A |
| 2 |
| 2π |
| 9 |
(Ⅰ)求φ的值;
(Ⅱ)若PQ⊥PR,求A的值.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:计算题,三角函数的图像与性质
分析:第(Ⅰ)问要求φ值,要先求出φ的某种三角函数值,代入P点坐标即可,结合图象和φ的取值范围确定φ的值;第(Ⅱ)问要根据PQ⊥PR,求出P、Q、R点的坐标,然后利用向量的内积为0构建关于A的方程求解.
解答:
(本小题14分)
解:(I)∵函数经过点P(0,
)∴sinφ=
…(3分)
又∵φ∈[0,2π),且点P在递减区间上∴ϕ=
…(7分)
(II)由(I)可知y=Asin(
+
)令y=0,得sin(
x+
)=0
∴
x+
=0∴x=-
∴Q(-
,0)…(9分)
令y=-A,得sin(
x+
)=-1∴
x+
=
∴x=3∴R(3,-A)…(11分)
又∵P(0,
),∴
=(-
,-
),
=(3,-
)
∵PQ⊥PR,∴
•
=-
+
A2=0解得:A=
…(14分)
解:(I)∵函数经过点P(0,
| A |
| 2 |
| 1 |
| 2 |
又∵φ∈[0,2π),且点P在递减区间上∴ϕ=
| 5π |
| 6 |
(II)由(I)可知y=Asin(
| 2π |
| 9 |
| 5π |
| 6 |
| 2π |
| 9 |
| 5π |
| 6 |
∴
| 2π |
| 9 |
| 5π |
| 6 |
| 15 |
| 4 |
| 15 |
| 4 |
令y=-A,得sin(
| 2π |
| 9 |
| 5π |
| 6 |
| 2π |
| 9 |
| 5π |
| 6 |
| 3π |
| 2 |
又∵P(0,
| A |
| 2 |
| PQ |
| 15 |
| 4 |
| A |
| 2 |
| PR |
| 3A |
| 2 |
∵PQ⊥PR,∴
| PQ |
| PR |
| 45 |
| 4 |
| 3 |
| 4 |
| 15 |
点评:本题综合性较强,重点考查了三角函数的图象与性质,在解题中利用了数形结及方程的思想.

练习册系列答案
相关题目
已知等差数列{an}单调递增且满足a1+a10=4,则a8的取值范围是( )
| A、(2,4) |
| B、(-∞,2) |
| C、(2,+∞) |
| D、(4,+∞) |