题目内容
四个顶点都在球O上的四面体ABCD所有棱长都为12，点E、F分别为棱AB、AC的中点，则球O截直线EF所得弦长为（ ）
A、6
| ||
| B、12 | ||
C、6
| ||
D、6
|
考点：球内接多面体,球的体积和表面积
专题：综合题,空间位置关系与距离
分析：把四面体补成正方体，两者的外接球是同一个，求出正方体的棱长，然后求出正方体的对角线长，可得正四面体的外接球的半径，求出球心到EF的距离，即可求出球O截直线EF所得弦长．
解答：
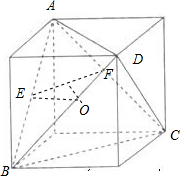解：如图，将四面体补成正方体，则正方体的棱长是6
，正方体的对角线长为：6
，
正四面体的外接球的半径为：3
．
设球心为O，O到EF的距离为d，则d=
=3．
∴O截直线EF所得弦长为2
=6
．
故选：A．
解：如图，将四面体补成正方体，则正方体的棱长是6| 2 |
| 6 |
正四面体的外接球的半径为：3
| 6 |
设球心为O，O到EF的距离为d，则d=
(3
|
∴O截直线EF所得弦长为2
(3
|
| 5 |
故选：A．
点评：本题是基础题，考查空间想象能力，正四面体的外接球转化为正方体外接球，使得问题的难度得到降低，问题得到解决，注意正方体的对角线就是球的直径，也是比较重要的．
练习册系列答案
七星图书口算速算天天练系列答案
相关题目
已知点F1、F2是椭圆
+
=1的左、右焦点，过F2作倾斜角为
的直线交椭圆于A、B两点，则S △F1AB=（ ）
| x2 |
| 2 |
| y2 |
| 1 |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f（x）=k-
（k＞0）有且仅有两个不同的零点θ，φ（θ＞φ），则以下有关两零点关系的结论正确的是（ ）
| sin|x| |
| x |
| A、sinφ=φcosθ |
| B、sinφ=-φcosθ |
| C、sinθ=θcosφ |
| D、sinθ=-θcosφ |
已知双曲线
-
=1（a＞0，b＞0）的离心率为2．F1、F2分别是它的左、右焦点，点A是它的右顶点．过F1作一条斜率为k（k≠0）的直线与双曲线交于两个点M、N．则∠MAN=（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、30° | B、45° |
| C、60° | D、90° |
己知双曲线
-
=1（a＞0，b＞0）离心率为2，有一个焦点与抛物线y2=4x的焦点重合，则
的值为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知M（x，y）落在双曲线
-
=1的两条渐近线与抛物线y2=-2px（p＞0）的准线所围成的封闭区域（包括边界）内，且点M的坐标（x，y）满足x+2y+a=0．若a的最大值为2
-2，则p为（ ）
| y2 |
| 3 |
| x2 |
| 2 |
| 6 |
| A、2 | B、4 | C、8 | D、16 |
正三角形ABC的边长为2，将它沿高AD翻折，使点B与点C间的距离为
，此时四面体ABCD的外接球的表面积为（ ）
| 2 |
| A、6π | ||
B、
| ||
| C、5π | ||
D、
|