题目内容
已知M(x,y)落在双曲线
-
=1的两条渐近线与抛物线y2=-2px(p>0)的准线所围成的封闭区域(包括边界)内,且点M的坐标(x,y)满足x+2y+a=0.若a的最大值为2
-2,则p为( )
| y2 |
| 3 |
| x2 |
| 2 |
| 6 |
| A、2 | B、4 | C、8 | D、16 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据双曲线的渐近线公式和抛物线准线的公式,求出三条直线方程,从而得到可行域是图中△ABO及其内部,然后利用直线平移法,即可求得结论.
解答:
 解:双曲线
解:双曲线
-
=1的渐近线方程为y=±
x,抛物线y2=-2px的准线为x=
,
∴抛物线y2=-8x的准线为x=2,
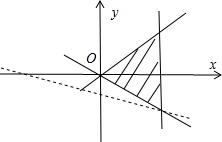
因此作出三条直线,得可行域是△ABO及其内部(如图)
将直线l:y=-
x-
进行平移,可得
当直线y=-
x-
过点(
,-
p)时,目标函数a=-x-2y有最大值
∴amax=-
+
p=2
-2,
∴p=4
故选:B.
 解:双曲线
解:双曲线| y2 |
| 3 |
| x2 |
| 2 |
| ||
| 2 |
| p |
| 2 |
∴抛物线y2=-8x的准线为x=2,
因此作出三条直线,得可行域是△ABO及其内部(如图)
将直线l:y=-
| 1 |
| 2 |
| a |
| 2 |
当直线y=-
| 1 |
| 2 |
| a |
| 2 |
| p |
| 2 |
| ||
| 4 |
∴amax=-
| p |
| 2 |
| ||
| 2 |
| 6 |
∴p=4
故选:B.
点评:本题以简单的线性规划为载体,求目标函数的最大值,着重考查了双曲线、抛物线的标准方程和基本概念和简单的线性规划等知识,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=ex+x2-x,若对任意x1,x2∈[-1,1],|f(x1)-f(x2)|≤k恒成立,则k的取值范围是( )
| A、[e-1,+∞) |
| B、[e,+∞) |
| C、[e+1,+∞) |
| D、[1,+∞) |
四个顶点都在球O上的四面体ABCD所有棱长都为12,点E、F分别为棱AB、AC的中点,则球O截直线EF所得弦长为( )
A、6
| ||
| B、12 | ||
C、6
| ||
D、6
|
已知数列{an}满足a1=1,an=an-12-1(n>2,n∈N*),则a3的值为( )
| A、0 | ||
| B、-1 | ||
| C、1 | ||
D、
|
已知椭圆
+x2=1与抛物线x2=ay有相同的焦点F,O为原点,点P是抛物线准线上一动点,点A在抛物线上,且|AF|=4,则|PA|+|PO|的最小值为( )
| y2 |
| 5 |
A、2
| ||
B、4
| ||
C、3
| ||
D、4
|
对于有线性相关关系的变量x,y,测得一组数据如表:
根据表,利用最小二乘法得它们的回归直线方程为
=8.5x+
,据此模型来预测x=20时,y的估计值是( )
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 60 | 70 |
 |
| y |
 |
| a |
| A、170 | B、175.5 |
| C、177.5 | D、212.5 |
在四面体ABCD中,∠ABC=∠ABD=∠ADC=
,则下列是直角的为( )
| π |
| 2 |
| A、∠BCD | B、∠BDC |
| C、∠CBD | D、∠ACD |