题目内容
7.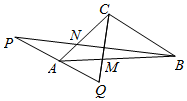 如图,在△ABC中,在AC上取点N,使得AN=$\frac{1}{3}$AC,在AB上取点M,使得AM=$\frac{1}{3}$AB,在BN的延长线上取点P,使得NP=$\frac{1}{2}$BN,延长PA,在CM的延长线取一点Q,若$\overrightarrow{AP}$=$\overrightarrow{QA}$,$\overrightarrow{MQ}$=λ$\overrightarrow{CM}$,试确定λ的值.
如图,在△ABC中,在AC上取点N,使得AN=$\frac{1}{3}$AC,在AB上取点M,使得AM=$\frac{1}{3}$AB,在BN的延长线上取点P,使得NP=$\frac{1}{2}$BN,延长PA,在CM的延长线取一点Q,若$\overrightarrow{AP}$=$\overrightarrow{QA}$,$\overrightarrow{MQ}$=λ$\overrightarrow{CM}$,试确定λ的值.
分析 由△APN∽△CBN得AP平行且等于BC的一半,故AQ平行且等于BC的一半,从而△AQM∽△BCM,得出MQ=$\frac{1}{2}$CM.
解答 解:∵AN=$\frac{1}{3}$AC,∴AN=$\frac{1}{2}$NC,又∵NP=$\frac{1}{2}$BN,∴△APN∽△CBN,∴AP∥BC,AP=$\frac{1}{2}$BC.
∵$\overrightarrow{AP}=\overrightarrow{QA}$,∴AQ=$\frac{1}{2}$BC,AQ∥BC,又∵AM=$\frac{1}{3}$AB,∴AM=$\frac{1}{2}$MB,∴△AQM∽△BCM,
∴MQ=$\frac{1}{2}$CM.∴λ=$\frac{1}{2}$.
点评 本题考查了平面向量的基本定理,相似三角形的应用,属于基础题.

练习册系列答案
相关题目
17.某船开始看见灯塔在南偏东30°方向,船沿南偏东60°的方向航行30n mile后看见灯塔在正西方向,则这时船与灯塔的距离是( )
| A. | 10$\sqrt{3}$n mile | B. | 20$\sqrt{3}$n mile | C. | 10$\sqrt{2}$n mile | D. | 20$\sqrt{2}$n mile |
18.若A∈a,B∈a,C是AB上任意一点,则下列结论错误的是( )
| A. | AC?a | B. | BC?a | C. | C?a | D. | C∈a |
12.cos$\frac{3π}{4}$等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |