题目内容
2．已知${∫}_{0}^{t}$xdx=2，求t的值．分析 利用定积分列出方程，即可求解t的值．
解答 解：${∫}_{0}^{t}$xdx=2，
可得t2=4，解得t=2，（t＞0）．
点评 本题考查定积分的应用，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知甲、乙两组数据如茎叶图所示，其中m∈（0，1，2，3，4，5，6，7，8，9），则甲的平均数不小于乙的平均数的概率为$\frac{3}{10}$．
17．若f（x）=3-x，则f′（0）=（ ）
| A． | 1 | B． | log3e | C． | ln3 | D． | -ln3 |
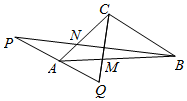如图，在△ABC中，在AC上取点N，使得AN=$\frac{1}{3}$AC，在AB上取点M，使得AM=$\frac{1}{3}$AB，在BN的延长线上取点P，使得NP=$\frac{1}{2}$BN，延长PA，在CM的延长线取一点Q，若$\overrightarrow{AP}$=$\overrightarrow{QA}$，$\overrightarrow{MQ}$=λ$\overrightarrow{CM}$，试确定λ的值．
14．已知平面α的法向量为（2，-4，-2），平面β的法向量为（-1，2，k），若α∥β，则k=﹙）
| A． | -2 | B． | -1 | C． | 1 | D． | 2 |