题目内容
17.某船开始看见灯塔在南偏东30°方向,船沿南偏东60°的方向航行30n mile后看见灯塔在正西方向,则这时船与灯塔的距离是( )| A. | 10$\sqrt{3}$n mile | B. | 20$\sqrt{3}$n mile | C. | 10$\sqrt{2}$n mile | D. | 20$\sqrt{2}$n mile |
分析 作出图形,根据方位角计算三角形的内角,利用正弦定理计算.
解答 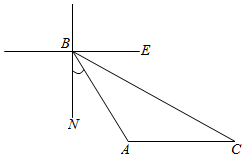 解设灯塔为A,船从B处航行至C处,则∠NBA=30°,∠NBC=60°,BC=30,
解设灯塔为A,船从B处航行至C处,则∠NBA=30°,∠NBC=60°,BC=30,
∴∠ABC=30°,∠EBC=30°,
∵AC∥BE,∴∠C=∠EBC=30°,∴△ABC是等腰三角形.∠A=120°.
在△ABC中,由正弦定理得$\frac{BC}{sinA}=\frac{AC}{sin∠ABC}$,即$\frac{30}{\frac{\sqrt{3}}{2}}=\frac{AC}{\frac{1}{2}}$,解得AC=10$\sqrt{3}$.
故选:A.
点评 本题考查了正弦定理,解三角形的实际应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.若集合A={x|x-1<0},B={x|-2<x<2},则A∩B等于( )
| A. | (-1,2) | B. | (0,2) | C. | (-2,1) | D. | (-2,-1) |
8.当0<a<1时,不等式loga(4-x)>-log${\;}_{\frac{1}{a}}$x的解集是( )
| A. | (0,+∞) | B. | (0,2) | C. | (2,4) | D. | (0,4) |
 已知甲、乙两组数据如茎叶图所示,其中m∈(0,1,2,3,4,5,6,7,8,9),则甲的平均数不小于乙的平均数的概率为$\frac{3}{10}$.
已知甲、乙两组数据如茎叶图所示,其中m∈(0,1,2,3,4,5,6,7,8,9),则甲的平均数不小于乙的平均数的概率为$\frac{3}{10}$. 如图,锐角三角形ABC中,角A,B,C所对的边分别为a,b,c.若2bcosB=a•cosC+c•cosA
如图,锐角三角形ABC中,角A,B,C所对的边分别为a,b,c.若2bcosB=a•cosC+c•cosA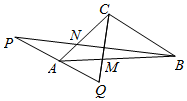 如图,在△ABC中,在AC上取点N,使得AN=$\frac{1}{3}$AC,在AB上取点M,使得AM=$\frac{1}{3}$AB,在BN的延长线上取点P,使得NP=$\frac{1}{2}$BN,延长PA,在CM的延长线取一点Q,若$\overrightarrow{AP}$=$\overrightarrow{QA}$,$\overrightarrow{MQ}$=λ$\overrightarrow{CM}$,试确定λ的值.
如图,在△ABC中,在AC上取点N,使得AN=$\frac{1}{3}$AC,在AB上取点M,使得AM=$\frac{1}{3}$AB,在BN的延长线上取点P,使得NP=$\frac{1}{2}$BN,延长PA,在CM的延长线取一点Q,若$\overrightarrow{AP}$=$\overrightarrow{QA}$,$\overrightarrow{MQ}$=λ$\overrightarrow{CM}$,试确定λ的值.