题目内容
已知
为单位矩阵,且α、β∈[
,π],则tan(α+β)= .
|
| π |
| 2 |
考点:二阶矩阵,两角和与差的正切函数
专题:选作题,矩阵和变换
分析:利用单位矩阵是个方阵,除左上角到右下角的对角线(称为主对角线)上的元素均为1以外全都为0,即可求出tan(α+β).
解答:
解:∵
为单位矩阵,
∴sinα=1,-
cosβ=1,
∵α、β∈[
,π],
∴α=
,β=
,
∴tan(α+β)=tan(
+
)=1
故答案为:1
|
∴sinα=1,-
| 2 |
∵α、β∈[
| π |
| 2 |
∴α=
| π |
| 2 |
| 3π |
| 4 |
∴tan(α+β)=tan(
| π |
| 2 |
| 3π |
| 4 |
故答案为:1
点评:单位矩阵是个方阵,除左上角到右下角的对角线(称为主对角线)上的元素均为1以外全都为0.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知数列{an}是等比数列,若a2a3a4=64,
=16,则(
)-2×2-3-(a5)
=( )
| a6a8 |
| 1 |
| 4 |
| 1 |
| 3 |
| A、4 | ||
| B、0 | ||
| C、0或-4 | ||
D、-
|
 如图,圆O为等腰梯形ABCD的外接圆,且AB∥CD,过点C作圆的切线CE交AB的延长线于E,证明:
如图,圆O为等腰梯形ABCD的外接圆,且AB∥CD,过点C作圆的切线CE交AB的延长线于E,证明: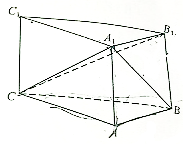 如图,在三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠CAB=90°,AC=2,BC=
如图,在三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠CAB=90°,AC=2,BC=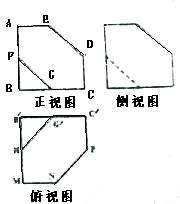 用一平面截棱长为2的正方体,截得的多面体的三视图如图所示,ABCDE,B′MNPC′是边长为2的正方形的一角,其中AE=CD=MN=PC′=1,F,G,H,G′分别是所在各边的中点,其侧视图与正视图尺寸相同,则该多面体的体积是( )
用一平面截棱长为2的正方体,截得的多面体的三视图如图所示,ABCDE,B′MNPC′是边长为2的正方形的一角,其中AE=CD=MN=PC′=1,F,G,H,G′分别是所在各边的中点,其侧视图与正视图尺寸相同,则该多面体的体积是( )