题目内容
13.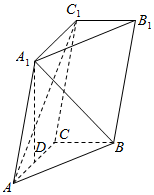 如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.(1)证明:AC1⊥A1B;
(2)设二面角A1-AB-C的正切值为$\sqrt{15}$.求直线AA1与平面BCC1B1的距离.
分析 (1)推导出平面AA1C1C⊥平面ABC,从而BC⊥平面AA1C1C,再求出AC1⊥A1C,由此能证明AC1⊥A1B.
(2)推导出平面AA1C1C⊥平面BCC1B1.作A1E⊥CC1,E为垂足,作DF⊥AB,F为垂足,连接A1F.得到∠A1FD为二面角A1-AB-C的平面角.由此能求出直线AA1与平面BCC1B1的距离.
解答 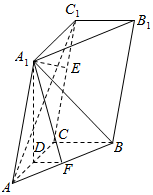 证明:(1)因为A1D⊥平面ABC,A1D?平面AA1C1C,
证明:(1)因为A1D⊥平面ABC,A1D?平面AA1C1C,
故平面AA1C1C⊥平面ABC,
又BC⊥AC,所以BC⊥平面AA1C1C,连接A1C.
因为侧面AA1C1C为菱形,故AC1⊥A1C.
由三垂线定理得AC1⊥A1B.
解:(2)BC⊥平面AA1C1C,BC?平面BCC1B1.
故平面AA1C1C⊥平面BCC1B1.
作A1E⊥CC1,E为垂足,则A1E⊥平面BCC1B1.
作DF⊥AB,F为垂足,连接A1F.
由三垂线定理得A1F⊥AB,
故∠A1FD为二面角A1-AB-C的平面角.
设AD=x则A1D=$\sqrt{4-{x^2}}$,$DF=\frac{{\sqrt{5}}}{5}x$,而tan∠A1FD=$\frac{A1D}{DF}$=$\sqrt{15}$,
故x=1,所以D是AC的中点,
故${A_1}D=\sqrt{3}$为直线AA1与平面BCC1B1的距离.
点评 本题考查异面直线垂直的证明,考查直线到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
4.设函数$f(x)=\left\{{\begin{array}{l}{{4^{{{log}_2}(x-8)}}(x≥9)}\\{2{x^2}-x-8(x<9)}\end{array}}\right.$,若f(t)=4,则t的值为( )
| A. | 10 | B. | 6或10 | C. | 6 | D. | 不存在 |
18.设点(a,b)是区域$\left\{\begin{array}{l}x+y-4≤0\\ x>0\\ y>0\end{array}$内的任意一点,则使函数f(x)=ax2-2bx+3在区间[$\frac{1}{2}$,+∞)上是增函数的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
2.已知实数x,y满足约束条件$\left\{\begin{array}{l}x+2y≤6\\ 2x-y≤6\\ x≥0,y≥0\end{array}\right.$则x-3y>0的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
 已知等腰梯形ABCD(如图(1)所示),其中AB∥CD,E,F分別为AB和CD的中点,且AB=EF=2,CD=6,M为BC中点.现将梯形ABCD沿着EF所在直线折起,使平面EFCB⊥平面EFDA(如图(2)所示),N是线段CD上一动点,且CN=$\frac{1}{2}$ND.
已知等腰梯形ABCD(如图(1)所示),其中AB∥CD,E,F分別为AB和CD的中点,且AB=EF=2,CD=6,M为BC中点.现将梯形ABCD沿着EF所在直线折起,使平面EFCB⊥平面EFDA(如图(2)所示),N是线段CD上一动点,且CN=$\frac{1}{2}$ND.