题目内容
4.设函数$f(x)=\left\{{\begin{array}{l}{{4^{{{log}_2}(x-8)}}(x≥9)}\\{2{x^2}-x-8(x<9)}\end{array}}\right.$,若f(t)=4,则t的值为( )| A. | 10 | B. | 6或10 | C. | 6 | D. | 不存在 |
分析 利用分段函数列出方程利用对数以及二次方程求解即可.
解答 解:当t<9时,f(t)=2t2-t+8=4⇒2t2-t+4=0,无解;
当t≥9时,$f(t)={4}^{lo{g}_{2}(t-8)}={2}^{lo{g}_{2}(t-8)^{2}}$=(t-8)2=4,解得t=6(舍去)或t=10.
故A项正确.
故选:A.
点评 本题考查分段函数的应用,函数与方程的解法,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.已知x是x1,x2,…,x10的平均值,a1为x1,x2,x3,x4的平均值,a2为x5,x6,x10的平均值,则x=( )
| A. | $\frac{2{a}_{1}+3{a}_{2}}{5}$ | B. | $\frac{3{a}_{1}+2{a}_{2}}{5}$ | C. | a1+a2 | D. | $\frac{{a}_{1}+{a}_{2}}{2}$ |
16.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左、右焦点分别为F1、F2,过F2的直线交双曲线于P,Q两点且PQ⊥PF1,若|PQ|=λ|PF1|,$\frac{5}{12}≤λ≤\frac{4}{3}$,则双曲线离心率e的取值范围为( )
| A. | $(1,\frac{{\sqrt{10}}}{2}]$ | B. | $(1,\frac{{\sqrt{37}}}{5}]$ | C. | $[\frac{{\sqrt{37}}}{5},\frac{{\sqrt{10}}}{2}]$ | D. | $[\frac{{\sqrt{10}}}{2},+∞)$ |
14.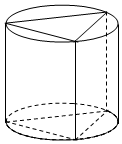 如图,圆柱内有一个三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形,圆柱侧面积为16π,其底面直径与母线长相等,则此三棱柱的体积为( )
如图,圆柱内有一个三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形,圆柱侧面积为16π,其底面直径与母线长相等,则此三棱柱的体积为( )
 如图,圆柱内有一个三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形,圆柱侧面积为16π,其底面直径与母线长相等,则此三棱柱的体积为( )
如图,圆柱内有一个三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形,圆柱侧面积为16π,其底面直径与母线长相等,则此三棱柱的体积为( )| A. | 6$\sqrt{3}$ | B. | 12 | C. | 12$\sqrt{3}$ | D. | 16$\sqrt{3}$ |
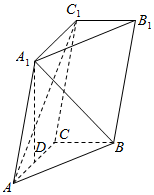 如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.