题目内容
18.设点(a,b)是区域$\left\{\begin{array}{l}x+y-4≤0\\ x>0\\ y>0\end{array}$内的任意一点,则使函数f(x)=ax2-2bx+3在区间[$\frac{1}{2}$,+∞)上是增函数的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
分析 作出不等式组对应的平面区域,求出函数f(x)=ax2-2bx+3在区间[$\frac{1}{2}$,+∞)上是增函数的等价条件,求出对应的面积,根据几何概型的概率公式进行求解即可.
解答  解:作出不等式组对应的平面区域如图
解:作出不等式组对应的平面区域如图
若f(x)=ax2-2bx+3在区间[$\frac{1}{2}$,+∞)上是增函数,
则$\left\{\begin{array}{l}{a>0}\\{-\frac{-2b}{2a}=\frac{b}{a}≤\frac{1}{2}}\end{array}\right.$,即$\left\{\begin{array}{l}{a>0}\\{a-2b≥0}\end{array}\right.$,
则A(0,4),B(4,0),由$\left\{\begin{array}{l}{a+b-4=0}\\{a-2b=0}\end{array}\right.$得$\left\{\begin{array}{l}{a=\frac{8}{3}}\\{b=\frac{4}{3}}\end{array}\right.$,
即C($\frac{8}{3}$,$\frac{4}{3}$),
则△OBC的面积S=$\frac{1}{2}×4×$$\frac{4}{3}$=$\frac{8}{3}$.
△OAB的面积S=$\frac{1}{2}×4×$4=8.
则使函数f(x)=ax2-2bx+3在区间[$\frac{1}{2}$,+∞)上是增函数的概率P=$\frac{{S}_{△OBC}}{{S}_{△OAB}}$=$\frac{\frac{8}{3}}{8}=\frac{1}{3}$,
故选:A.
点评 本题主要考查几何概型的概率的概率公式,作出不等式组对应的平面区域,求出对应的面积是解决本题的关键.

| A. | [$\frac{1}{2},\sqrt{2}$) | B. | [$\frac{1}{2},\sqrt{2}$] | C. | [$\frac{\sqrt{2}}{2},\sqrt{2}$) | D. | [$\frac{\sqrt{2}}{2},\sqrt{2}$] |
| A. | (0,1) | B. | (0,$\frac{3}{2}$) | C. | (-∞,1) | D. | (-∞,$\frac{4}{3}$) |
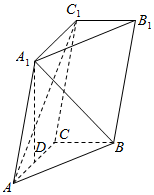 如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.