题目内容
2.已知实数x,y满足约束条件$\left\{\begin{array}{l}x+2y≤6\\ 2x-y≤6\\ x≥0,y≥0\end{array}\right.$则x-3y>0的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
分析 作出不等式组对应的平面区域,求出对应区域的面积,利用几何概型的概率公式进行求解即可.
解答 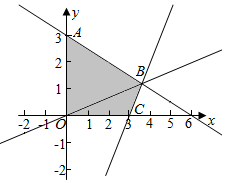 解:作出不等式组对应的平面区域如图(阴影部分):
解:作出不等式组对应的平面区域如图(阴影部分):
则A(0,3),C(3,0)
由$\left\{\begin{array}{l}{x+2y=6}\\{2x-y=6}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{18}{5}}\\{y=\frac{6}{5}}\end{array}\right.$,即B($\frac{18}{5}$,$\frac{6}{5}$),
作出直线x-3y=0,则直线过B,
则x-3y>0对应的区域为△OBC,
则△OBC的面积S△OBC=$\frac{1}{2}×3×$$\frac{6}{5}$=$\frac{9}{5}$,
△OAB的面积S△OAB=$\frac{1}{2}×3×$$\frac{18}{5}$=$\frac{27}{5}$,
则四边形OABC的面积S=$\frac{9}{5}$+$\frac{27}{5}$=$\frac{36}{5}$,
则x-3y>0的概率是$\frac{\frac{9}{5}}{\frac{36}{5}}$=$\frac{1}{4}$,
故选:A.
点评 本题主要考查几何概型的概率的计算,作出不等式组对应的平面区域,求出对应的面积,利用面积之间的关系是解决本题的关键.

练习册系列答案
相关题目
17.若在区间[0,π]上随机取一个数x,则sinx的值落在区间($\frac{1}{2}$,1)内的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{π}$ |
7.已知函数f(x)=(ex+1)(ax+2a-2),若存在x∈(0,+∞),使得不等式f(x)-2<0成立,则实数a的取值范围是( )
| A. | (0,1) | B. | (0,$\frac{3}{2}$) | C. | (-∞,1) | D. | (-∞,$\frac{4}{3}$) |
14.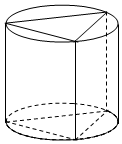 如图,圆柱内有一个三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形,圆柱侧面积为16π,其底面直径与母线长相等,则此三棱柱的体积为( )
如图,圆柱内有一个三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形,圆柱侧面积为16π,其底面直径与母线长相等,则此三棱柱的体积为( )
 如图,圆柱内有一个三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形,圆柱侧面积为16π,其底面直径与母线长相等,则此三棱柱的体积为( )
如图,圆柱内有一个三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形,圆柱侧面积为16π,其底面直径与母线长相等,则此三棱柱的体积为( )| A. | 6$\sqrt{3}$ | B. | 12 | C. | 12$\sqrt{3}$ | D. | 16$\sqrt{3}$ |
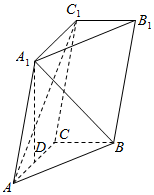 如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.