题目内容
8.过定点P(1,2)的直线$\left\{\begin{array}{l}{x=1+\frac{\sqrt{3}}{2}t}\\{y=2+\frac{1}{2}t}\end{array}\right.$(t为参数),与圆x2+y2=4相交于A、B两点.则|AB|=$\sqrt{3+4\sqrt{3}}$.分析 将直线的参数方程代入圆的方程,利用参数的几何意义和根与系数的关系计算|AB|.
解答 解:把$\left\{\begin{array}{l}{x=1+\frac{\sqrt{3}}{2}t}\\{y=2+\frac{1}{2}t}\end{array}\right.$(t为参数)代入x2+y2=4得:t2+($\sqrt{3}+2$)t+1=0.
∴t1+t2=-($\sqrt{3}+2$),t1t2=1.
∴|AB|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$=$\sqrt{3+4\sqrt{3}}$.
故答案为$\sqrt{3+4\sqrt{3}}$.
点评 本题考查了直线的参数方程,参数的几何意义,属于中档题.

练习册系列答案
相关题目
5.已知x是x1,x2,…,x10的平均值,a1为x1,x2,x3,x4的平均值,a2为x5,x6,x10的平均值,则x=( )
| A. | $\frac{2{a}_{1}+3{a}_{2}}{5}$ | B. | $\frac{3{a}_{1}+2{a}_{2}}{5}$ | C. | a1+a2 | D. | $\frac{{a}_{1}+{a}_{2}}{2}$ |
16.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左、右焦点分别为F1、F2,过F2的直线交双曲线于P,Q两点且PQ⊥PF1,若|PQ|=λ|PF1|,$\frac{5}{12}≤λ≤\frac{4}{3}$,则双曲线离心率e的取值范围为( )
| A. | $(1,\frac{{\sqrt{10}}}{2}]$ | B. | $(1,\frac{{\sqrt{37}}}{5}]$ | C. | $[\frac{{\sqrt{37}}}{5},\frac{{\sqrt{10}}}{2}]$ | D. | $[\frac{{\sqrt{10}}}{2},+∞)$ |
17.若在区间[0,π]上随机取一个数x,则sinx的值落在区间($\frac{1}{2}$,1)内的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{π}$ |
18.下列函数中,在其定义域内既是奇函数又是单调递增的函数是( )
| A. | y=-$\frac{1}{x}$ | B. | y=3-x-3x | C. | y=x|x| | D. | y=x3-x |
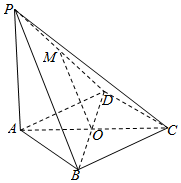 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,AB=2,∠BAD=60°,M是PD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,AB=2,∠BAD=60°,M是PD的中点.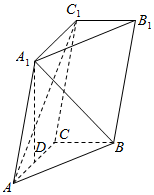 如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.