题目内容
5.已知函数f(x)=asinωx+bcosωx+1(a,b≠0,ω>0)的最小正周期是π.f(x)有最大值7$\frac{1}{2}$,且f($\frac{π}{6}$)=$\frac{5\sqrt{3}}{4}$+4(1)求a,b的值(2)若α≠kπ+β,(k∈Z),且α,β是f(x)=0的两根,求tan(α+β)的值.
分析 (1)根据辅助角公式f(x)=$\sqrt{{a}^{2}+{b}^{2}}$sin(ωx+φ)+1,f(x)有最大值7$\frac{1}{2}$,$\sqrt{{a}^{2}+{b}^{2}}$=6$\frac{1}{2}$,
f($\frac{π}{6}$)=$\frac{5\sqrt{3}}{4}$+4,a+$\frac{1}{2}$b=$\frac{5\sqrt{3}}{4}$+3,联立求得a、b的值,
(2)根据和差化积公式改写成cos(α+β+φ)sin(α-β)=0,α≠kπ+β,(k∈Z),sin(α-β)≠0,cos(α+β+φ)=0,求得α+β=kπ+$\frac{π}{2}$-φ(k∈Z),再求得tan(α+β).
解答 解:(1)f(x)=asinωx+bcosωx+1=$\sqrt{{a}^{2}+{b}^{2}}$sin(ωx+φ)+1,
最小正周期是π,ω=$\frac{2π}{T}$=2,
f(x)有最大值7$\frac{1}{2}$,$\sqrt{{a}^{2}+{b}^{2}}$=6$\frac{1}{2}$,①
f($\frac{π}{6}$)=$\frac{5\sqrt{3}}{4}$+4,
asin$\frac{π}{3}$+bcos$\frac{π}{3}$+1=$\frac{5\sqrt{3}}{4}$+4,
$\frac{\sqrt{3}}{2}$a+$\frac{1}{2}$b=$\frac{5\sqrt{3}}{4}$+3,②
联立①②解得:a=$\frac{5}{2}$,b=6,
∴a=$\frac{5}{2}$,b=6,
(2)tanφ=$\frac{12}{5}$,f(x)=6$\frac{1}{2}$sin(2x+φ)+1,
α,β是f(x)=0的两根,f(α)=f(β)=0,
sin(2α+φ)-sin(2β+φ)=0.
∴cos(α+β+φ)sin(α-β)=0,
α≠kπ+β,(k∈Z),sin(α-β)≠0,
α+β=kπ+$\frac{π}{2}$-φ(k∈Z).
∴tan(α+β)=tan($\frac{π}{2}$-φ)=$\frac{sin(\frac{π}{2}-φ)}{cos(\frac{π}{2}-φ)}$,
tan(α+β)=$\frac{cosφ}{sinφ}$=$\frac{1}{tanφ}$=$\frac{5}{12}$,
tan(α+β)=$\frac{5}{12}$.
点评 本题考查辅助角公式及积化和差公式,过程复杂,属于基础题.

| A. | $(1,\frac{{\sqrt{10}}}{2}]$ | B. | $(1,\frac{{\sqrt{37}}}{5}]$ | C. | $[\frac{{\sqrt{37}}}{5},\frac{{\sqrt{10}}}{2}]$ | D. | $[\frac{{\sqrt{10}}}{2},+∞)$ |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{π}$ |
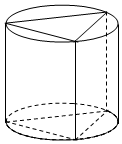 如图,圆柱内有一个三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形,圆柱侧面积为16π,其底面直径与母线长相等,则此三棱柱的体积为( )
如图,圆柱内有一个三棱柱,三棱柱的底面在圆柱底面内,且底面是正三角形,圆柱侧面积为16π,其底面直径与母线长相等,则此三棱柱的体积为( )| A. | 6$\sqrt{3}$ | B. | 12 | C. | 12$\sqrt{3}$ | D. | 16$\sqrt{3}$ |
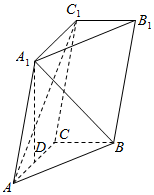 如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.