题目内容
已知
•
=0,向量
满足(
-
)•(
-
)=0,|
-
|=5,|
-
|=3,则
•
的最大值为 .
| a |
| b |
| c |
| c |
| a |
| c |
| b |
| a |
| b |
| a |
| c |
| a |
| c |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由
•
=0,建立如图所示的直角坐标系.可设
=(m,0),
=(0,n),
=(x,y),由|
-
|=5,m2+n2=25.记此圆为⊙M.根据向量
满足(
-
)•(
-
)=0,说明点C在⊙M上.
由|
|=|
-
|=3,可得|
|=|
-
|=4,过点C分别作CD⊥y轴,CE⊥x轴,垂足分别为D,E.设∠CBD=θ,则∠OAC=θ.可得x=4sinθ=m-3cosθ,
•
=mx=10sin(2θ-φ)+8,即可得出.
| a |
| b |
| a |
| b |
| c |
| a |
| b |
| c |
| c |
| a |
| c |
| b |
由|
| AC |
| c |
| a |
| BC |
| c |
| b |
| a |
| c |
解答:
解:由
•
=0,建立如图所示的直角坐标系.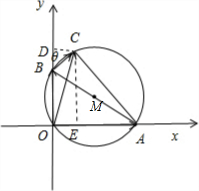
可设
=(m,0),
=(0,n),
=(x,y),
∵|
-
|=5,
∴m2+n2=25.记此圆为⊙M.
∵向量
满足(
-
)•(
-
)=0,
∴x2+y2-mx-ny=0,
化为(x-
)2+(y-
)2=
.
说明点C在⊙M上.
∴|
|=|
-
|=3,
∴|
|=|
-
|=4,
过点C分别作CD⊥y轴,CE⊥x轴,垂足分别为D,E.
设∠CBD=θ,则∠OAC=θ.
则x=4sinθ=m-3cosθ,
∵
•
=mx=4sinθ(4sinθ+3cosθ)
=16sin2θ+12sinθcosθ
=8(1-cos2θ)+6sin2θ
=10sin(2θ-φ)+8≤18.
∴
•
的最大值为18.
故答案为:18.
| a |
| b |

可设
| a |
| b |
| c |
∵|
| a |
| b |
∴m2+n2=25.记此圆为⊙M.
∵向量
| c |
| c |
| a |
| c |
| b |
∴x2+y2-mx-ny=0,
化为(x-
| m |
| 2 |
| n |
| 2 |
| 25 |
| 4 |
说明点C在⊙M上.
∴|
| AC |
| c |
| a |
∴|
| BC |
| c |
| b |
过点C分别作CD⊥y轴,CE⊥x轴,垂足分别为D,E.
设∠CBD=θ,则∠OAC=θ.
则x=4sinθ=m-3cosθ,
∵
| a |
| c |
=16sin2θ+12sinθcosθ
=8(1-cos2θ)+6sin2θ
=10sin(2θ-φ)+8≤18.
∴
| a |
| c |
故答案为:18.
点评:本题综合考查了向量的坐标运算、向量垂直与数量积的关系、数量积的性质、三角函数代换等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目

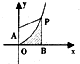 如图,已知点A(0,1),点P(x0,y0)(x0>0)在曲线y=x2上移动,过P点作PB⊥x轴于B,若曲线y=x2在第一象限内把梯形AOBP的面积平分,则P点的坐标为
如图,已知点A(0,1),点P(x0,y0)(x0>0)在曲线y=x2上移动,过P点作PB⊥x轴于B,若曲线y=x2在第一象限内把梯形AOBP的面积平分,则P点的坐标为 如图中的程序框图所描述的算法为欧几里得辗转相除法,若输入m=11077,n=2014,则输出m=
如图中的程序框图所描述的算法为欧几里得辗转相除法,若输入m=11077,n=2014,则输出m=