题目内容
12.将函数$y=sin({2x-\frac{π}{6}})$向右平移$\frac{π}{12}$个单位后得到y=g(x)的图象,若函数y=g(x)在区间[a,b](b>a)上的值域是$[{-\frac{1}{2},1}]$,则b-a的最小值m和最大值M分别为( )| A. | $m=\frac{π}{6},M=\frac{π}{3}$ | B. | $m=\frac{π}{3},M=\frac{2π}{3}$ | C. | $m=\frac{4π}{3},M=2π$ | D. | $m=\frac{2π}{3},M=\frac{4π}{3}$ |
分析 由已知利用函数y=Asin(ωx+φ)的图象变换规律可求g(x)的函数解析式,进而利用正弦函数的图象和性质即可求解.
解答 解:将函数$y=sin({2x-\frac{π}{6}})$向右平移$\frac{π}{12}$后,得到:$y=g(x)=sin[{2({x-\frac{π}{12}})-\frac{π}{6}}]=sin({2x-\frac{π}{3}})$,
由函数$g(x)=sin({2x-\frac{π}{3}})$的图象可知,
当函数的值域是$[{-\frac{1}{2},1}]$,最小值:$m=\frac{5π}{12}-\frac{π}{12}=\frac{π}{3}$,最大值:$M=2m=\frac{2π}{3}$.
故选:B.
点评 本题主要考查了函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象和性质的综合应用,考查了数形结合思想,熟练掌握正弦函数的图象和性质是解题的关键,属于中档题.

练习册系列答案
相关题目
3.某几何体的三视图如图所示,则该几何体的体积是( )
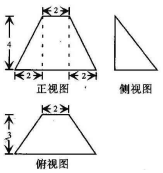

| A. | 16 | B. | 20 | C. | 52 | D. | 60 |
20.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,O为坐标原点,点P是双曲线在第一象限内的点,直线PO,PF2分别交双曲线C的左、右支于另一点M,N,若|PF1|=2|PF2|,且∠MF2N=120°,则双曲线的离心率为( )
| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\sqrt{7}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
7. 某三棱锥的三视图如图所示,其中三个视图都是直角三角形,则该三棱锥外接球的体积为( )
某三棱锥的三视图如图所示,其中三个视图都是直角三角形,则该三棱锥外接球的体积为( )
 某三棱锥的三视图如图所示,其中三个视图都是直角三角形,则该三棱锥外接球的体积为( )
某三棱锥的三视图如图所示,其中三个视图都是直角三角形,则该三棱锥外接球的体积为( )| A. | 2π | B. | $\sqrt{6}π$ | C. | 6π | D. | $4\sqrt{3}π$ |
17.命题“?x0∈R,x03-x02+1>0”的否定是( )
| A. | ?x0∈R,x${\;}_{0}^{3}$-x${\;}_{0}^{2}$+1<0 | B. | ?x∈R,x3-x2+1≤0 | ||
| C. | ?x0∈R,x${\;}_{0}^{3}$-x${\;}_{0}^{2}$+1≤0 | D. | ?x∈R,x3-x2+1>0 |
4.某几何体三视图如图所示,则该几何体的表面积为( )
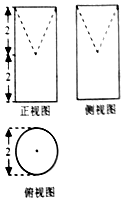

| A. | (9+$\sqrt{5}$)π | B. | (9+2$\sqrt{5}$)π | C. | (10+$\sqrt{5}$)π | D. | (10+2$\sqrt{5}$)π |
2.统计某产品的广告费用x与销售额y的一组数据如表:
若根据如表提供的数据用最小二乘法可求得y对x的回归直线方程是$\stackrel{∧}{y}$=1.1x+4.6,则数据中的m的值应该是8.
| 广告费用x | 2 | 3 | 5 | 6 |
| 销售额y | 7 | m | 9 | 12 |