题目内容
17.命题“?x0∈R,x03-x02+1>0”的否定是( )| A. | ?x0∈R,x${\;}_{0}^{3}$-x${\;}_{0}^{2}$+1<0 | B. | ?x∈R,x3-x2+1≤0 | ||
| C. | ?x0∈R,x${\;}_{0}^{3}$-x${\;}_{0}^{2}$+1≤0 | D. | ?x∈R,x3-x2+1>0 |
分析 根据特称命题“?x0∈M,P(x0)成立”的否定是全称命题“?x∈M,¬P(x)成立”,写出即可.
解答 解:命题“?x0∈R,x${\;}_{0}^{3}$-x${\;}_{0}^{2}$+1>0”的否定是
“?x∈R,x3-x2+1≤0”.
故选:B.
点评 本题考查了特称命题的否定是全称命题的应用问题,是基础题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
5.一个几何体的三视图如图所示,则该几何体的体积为( )
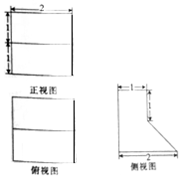

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
12.将函数$y=sin({2x-\frac{π}{6}})$向右平移$\frac{π}{12}$个单位后得到y=g(x)的图象,若函数y=g(x)在区间[a,b](b>a)上的值域是$[{-\frac{1}{2},1}]$,则b-a的最小值m和最大值M分别为( )
| A. | $m=\frac{π}{6},M=\frac{π}{3}$ | B. | $m=\frac{π}{3},M=\frac{2π}{3}$ | C. | $m=\frac{4π}{3},M=2π$ | D. | $m=\frac{2π}{3},M=\frac{4π}{3}$ |
6.已知集合M={x∈Z|x(x-3)≤0},N={x|lnx<1},则M∩N=( )
| A. | {1,2} | B. | {2,3} | C. | {0,1,2} | D. | {1,2,3} |
7.已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1(a>b>0)上一点A关于原点的对称点为点B,F为其右焦点,若AF⊥BF,设∠ABF=α,且
α∈[$\frac{π}{6}$,$\frac{π}{4}$],则该椭圆离心率e的取值范围为( )
α∈[$\frac{π}{6}$,$\frac{π}{4}$],则该椭圆离心率e的取值范围为( )
| A. | [$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$] | B. | [$\frac{\sqrt{2}}{2}$,1) | C. | [$\frac{\sqrt{2}}{2}$,$\sqrt{3}$-1] | D. | [$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$] |