题目内容
2.统计某产品的广告费用x与销售额y的一组数据如表:| 广告费用x | 2 | 3 | 5 | 6 |
| 销售额y | 7 | m | 9 | 12 |
分析 先求样本中心点,再代入回归直线方程,即可求得m的值.
解答 解:由题意,$\overline{x}$=4,$\overline{y}$=7+$\frac{m}{4}$,
∵y对x的回归直线方程是$\stackrel{∧}{y}$=1.1x+4.6,
∴7+$\frac{m}{4}$=4.4+4.6,∴m=8,
故答案为8.
点评 本题考查回归直线方程,解题的关键是利用回归直线方程恒过样本中心点,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.将函数$y=sin({2x-\frac{π}{6}})$向右平移$\frac{π}{12}$个单位后得到y=g(x)的图象,若函数y=g(x)在区间[a,b](b>a)上的值域是$[{-\frac{1}{2},1}]$,则b-a的最小值m和最大值M分别为( )
| A. | $m=\frac{π}{6},M=\frac{π}{3}$ | B. | $m=\frac{π}{3},M=\frac{2π}{3}$ | C. | $m=\frac{4π}{3},M=2π$ | D. | $m=\frac{2π}{3},M=\frac{4π}{3}$ |
10.设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+m(m为常数),则f(-1)=( )
| A. | 3 | B. | 1 | C. | -1 | D. | -3 |
17.设双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左、右焦点分别为F1,F2,过F2的直线与双曲线的右支交于两点A,B,若|AF1|:|AB|=3:4,且F2是AB的一个四等分点,则双曲线C的离心率是( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{10}}}{2}$ | C. | $\frac{5}{2}$ | D. | 5 |
7.已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1(a>b>0)上一点A关于原点的对称点为点B,F为其右焦点,若AF⊥BF,设∠ABF=α,且
α∈[$\frac{π}{6}$,$\frac{π}{4}$],则该椭圆离心率e的取值范围为( )
α∈[$\frac{π}{6}$,$\frac{π}{4}$],则该椭圆离心率e的取值范围为( )
| A. | [$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$] | B. | [$\frac{\sqrt{2}}{2}$,1) | C. | [$\frac{\sqrt{2}}{2}$,$\sqrt{3}$-1] | D. | [$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$] |
12.已知F1,F2是双曲线的两个焦点,过F2作垂直于实轴的直线PQ交双曲线于P,Q两点,若∠PF1Q=$\frac{π}{2}$,则双曲线的离心率e等于( )
| A. | $\sqrt{2}$+2 | B. | $\sqrt{2}$+1 | C. | $\sqrt{2}$ | D. | $\sqrt{2}$-1 |
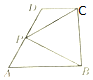 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设$\overrightarrow{AP}=x\overrightarrow{AD},\overrightarrow{PB}•\overrightarrow{PC}=y$,对于函数y=f(x),给出以下三个结论:①当a=2时,函数f(x)的值域为[1,4];②对于任意的a>0,均有f(1)=1;③对于任意的a>0,函数f(x)的最大值均为4.其中所有正确的结论序号为②③.
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设$\overrightarrow{AP}=x\overrightarrow{AD},\overrightarrow{PB}•\overrightarrow{PC}=y$,对于函数y=f(x),给出以下三个结论:①当a=2时,函数f(x)的值域为[1,4];②对于任意的a>0,均有f(1)=1;③对于任意的a>0,函数f(x)的最大值均为4.其中所有正确的结论序号为②③.