题目内容
4．某几何体三视图如图所示，则该几何体的表面积为（ ）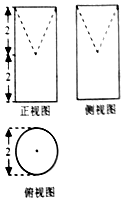
| A． | （9+$\sqrt{5}$）π | B． | （9+2$\sqrt{5}$）π | C． | （10+$\sqrt{5}$）π | D． | （10+2$\sqrt{5}$）π |
分析 由三视图得到几何体为圆柱挖去一个圆锥，根据图中数据求表面积．
解答 解：由三视图得到几何体为圆柱挖去一个圆锥，
圆柱的底面直径为2，高为4，
圆锥的底面直径为2，高为2，
所以几何体的表面积为π×12+π×2×4+$\frac{1}{2}×π×2×\sqrt{{2}^{2}+{1}^{2}}$=（9+$\sqrt{5}$）π；
故选A．
点评 本题考查了由几何体的三视图求对应几何体的表面积；关键是正确还原几何体．
练习册系列答案
相关题目
14．数列{an}满足a1=$\frac{{\sqrt{2}}}{8}$，a2=$\frac{{\sqrt{33}}}{33}$，（an＞0），$\frac{{{a}_{n}}^{2}-{{a}_{n-1}}^{2}}{{{a}_{n-1}}^{2}}$=$\frac{{{a}_{n+1}}^{2}-{{a}_{n}}^{2}}{{{a}_{n+1}}^{2}}$（n≥2），则a2017=（ ）
| A． | $\frac{{\sqrt{3}}}{64}$ | B． | $\frac{{\sqrt{2}}}{64}$ | C． | $\frac{1}{32}$ | D． | $\frac{33}{32}$ |
12．将函数$y=sin（{2x-\frac{π}{6}}）$向右平移$\frac{π}{12}$个单位后得到y=g（x）的图象，若函数y=g（x）在区间[a，b]（b＞a）上的值域是$[{-\frac{1}{2}，1}]$，则b-a的最小值m和最大值M分别为（ ）
| A． | $m=\frac{π}{6}，M=\frac{π}{3}$ | B． | $m=\frac{π}{3}，M=\frac{2π}{3}$ | C． | $m=\frac{4π}{3}，M=2π$ | D． | $m=\frac{2π}{3}，M=\frac{4π}{3}$ |
19．若x，y满足约束条件$\left\{\begin{array}{l}{x+y＞1}\\{x-y≥-1}\\{2x-y≤2}\end{array}\right.$，且目标函数z=ax+2y仅在点（1，0）处取得最小值，则a的取值范围是（ ）
| A． | （-1，2） | B． | （-4，2） | C． | （-4，0） | D． | （-4，2） |
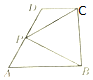如图，在直角梯形ABCD中，AB∥CD，AB⊥BC，AB=2，CD=1，BC=a（a＞0），P为线段AD（含端点）上一个动点，设$\overrightarrow{AP}=x\overrightarrow{AD}，\overrightarrow{PB}•\overrightarrow{PC}=y$，对于函数y=f（x），给出以下三个结论：①当a=2时，函数f（x）的值域为[1，4]；②对于任意的a＞0，均有f（1）=1；③对于任意的a＞0，函数f（x）的最大值均为4．其中所有正确的结论序号为②③．