题目内容
2.函数y=x3-x的单调增区间$(-∞,-\frac{{\sqrt{3}}}{3}),(\frac{{\sqrt{3}}}{3},+∞)$.分析 求函数的导数,利用f′(x)>0即可求出函数的单调递增区间.
解答 解:函数的导数f′(x)=3x2-1,
则有f′(x)>0得3x2-1>0,即x>$\frac{\sqrt{3}}{3}$或x<-$\frac{\sqrt{3}}{3}$,
即函数的单调递增区间为$(-∞,-\frac{{\sqrt{3}}}{3}),(\frac{{\sqrt{3}}}{3},+∞)$,
故答案为:$(-∞,-\frac{{\sqrt{3}}}{3}),(\frac{{\sqrt{3}}}{3},+∞)$
点评 本题主要考查函数单调区间的求解,求函数的导数利用导数法是解决本题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
13.如图是某几何体的三视图,则该几何体的体积为( )


| A. | 24 | B. | 36 | C. | 72 | D. | 144 |
10.2015年9月3日,抗战胜利70周年纪念活动在北京隆重举行,受到全国人民的瞩目.纪念活动包括举行纪念大会、阅兵式、招待会和文艺晚会等,据统计,抗战老兵由于身体原因,参加纪念大会、阅兵式、招待会这三个环节(可参加多个,也可都不参加)的情况及其概率如表所示:
(Ⅰ)若m=2n,则从这60名抗战老兵中按照参加纪念活动的环节数分层抽取6人进行座谈,求参加纪念活动环节数为2的抗战老兵中抽取的人数;
(Ⅱ)某医疗部门决定从(1)中抽取的6名抗战老兵中随机抽取2名进行体检,求这2名抗战老兵中至少有1人参加纪念活动的环节数为3的概率.
| 参加纪念活动的环节数 | 0 | 1 | 2 | 3 |
| 概率 | $\frac{1}{6}$ | m | n | $\frac{1}{3}$ |
(Ⅱ)某医疗部门决定从(1)中抽取的6名抗战老兵中随机抽取2名进行体检,求这2名抗战老兵中至少有1人参加纪念活动的环节数为3的概率.
7.已知m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
| A. | 若m?α,n?α,m∥β,n∥β,则α∥β | B. | 若m?α,m∥β,α∩β=n,则m∥n | ||
| C. | 若α∥β,m∥α,则m∥β | D. | 若m⊥n,n⊥β,β⊥α,则m⊥α |
11.一个圆内有一个内接等边三角形,一动点在圆内运动,则此点落在等边三角形内部的概率为( )
| A. | $\frac{3}{π}$ | B. | $\frac{{3\sqrt{3}}}{4π}$ | C. | $\frac{{\sqrt{3}}}{4π}$ | D. | $\frac{{2\sqrt{3}}}{3π}$ |
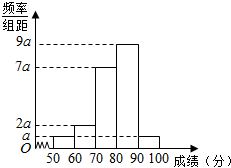 某中学举行电脑知识竞赛,对40名参赛选手考试成绩(单位:分)进行统计,发现他们的成绩分布在[50,60),[60,70),[70,80),[90,100),并得到如图所示的频率分布直方图
某中学举行电脑知识竞赛,对40名参赛选手考试成绩(单位:分)进行统计,发现他们的成绩分布在[50,60),[60,70),[70,80),[90,100),并得到如图所示的频率分布直方图