题目内容
3.点A是椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>1)的上顶点,B、C是该椭圆的另外两点,且△ABC是以点A为直角顶点的等腰直角三角形,若满足条件的△ABC只有一个,则椭圆的离心率e的范围是( )| A. | $\frac{\sqrt{3}}{3}$≤e<1 | B. | 0<e≤$\frac{\sqrt{3}}{3}$ | C. | 0<e≤$\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{3}$≤e<1 |
分析 由题意不妨设:直线AB的方程为:y=kx+1;直线AC的方程为:y=-$\frac{1}{k}$x+1.分别与椭圆方程联立可得|AB|,|AC|.由于|AC|=|BC|,化为
(|k|-1)[k2-(a2-1)|k|+1]=0,分别讨论即可得出.
解答 解:由题意不妨设:直线AB的方程为:y=kx+1;直线AC的方程为:y=-$\frac{1}{k}$x+1.
联立$\left\{\begin{array}{l}{y=kx+1}\\{\frac{{x}^{2}}{{a}^{2}}+{y}^{2}=1}\end{array}\right.$,化为:(a2k2+1)x2+2a2kx=0,解得x=0或x=$\frac{-2{a}^{2}k}{{a}^{2}{k}^{2}+1}$.
|AB|=$\frac{2{a}^{2}|k|\sqrt{1+{k}^{2}}}{{a}^{2}{k}^{2}+1}$,
联立$\left\{\begin{array}{l}{y=-\frac{1}{k}x+1}\\{\frac{{x}^{2}}{{a}^{2}}+{y}^{2}=1}\end{array}\right.$,可得|AC|=$\frac{2{a}^{2}|k|\sqrt{1+\frac{1}{{k}^{2}}}}{{a}^{2}+{k}^{2}}$.
∵|AC|=|AC|,
∴$\frac{2{a}^{2}|k|\sqrt{1+{k}^{2}}}{{a}^{2}{k}^{2}+1}$=$\frac{2{a}^{2}|k|\sqrt{1+\frac{1}{{k}^{2}}}}{{a}^{2}+{k}^{2}}$.
化为(|k|-1)[k2-(a2-1)|k|+1]=0,
当|k|-1=0,即k=±1时,此时满足条件的△ABC只有一个;
当k2-(a2-1)|k|+1=0时,
△=(a2+1)(a2-3),
当$1<a<\sqrt{3}$时,△<0,此时满足条件的△ABC只有一个;
$a=\sqrt{3}$时,△=0,|k|=1,此时满足条件的△ABC只有一个;
$a>\sqrt{3}$时,满足条件的△ABC有3个.
综上可得:1<a$≤\sqrt{3}$时,满足条件的△ABC只有一个.
∴e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{1-\frac{1}{{a}^{2}}}$∈$(0,\frac{\sqrt{6}}{3}]$.
故选:C.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、相互垂直的直线斜率之间的关系、等腰三角形的性质,考查了分类讨论方法、推理能力与计算能力,属于难题.

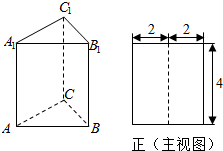 如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为4,且侧棱AA1⊥底面ABC,其正(主)视图是边长为4的正方形,则此三棱柱侧(左)视图的面积为( )
如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为4,且侧棱AA1⊥底面ABC,其正(主)视图是边长为4的正方形,则此三棱柱侧(左)视图的面积为( )| A. | 16 | B. | 4$\sqrt{3}$ | C. | 8$\sqrt{2}$ | D. | 8$\sqrt{3}$ |

| A. | 24 | B. | 36 | C. | 72 | D. | 144 |
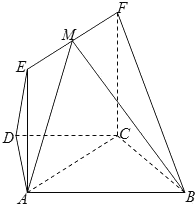 如图,平面ACFE⊥平面ABCD,四边形ACFE为矩形,在梯形ABCD中,AB∥CD,∠ABC=60°,且AD=DC=CB=AE=1,M是线段EF的中点.
如图,平面ACFE⊥平面ABCD,四边形ACFE为矩形,在梯形ABCD中,AB∥CD,∠ABC=60°,且AD=DC=CB=AE=1,M是线段EF的中点.