题目内容
3.若$\overrightarrow a=({2sin2x,-1}),\overrightarrow b=({{{sin}^2}x,sin2x})$,且函数$f(x)=\overrightarrow a•\overrightarrow b$,则f(x)是( )| A. | 最小正周期为$\frac{π}{2}$的奇函数 | B. | 最小正周期为π的奇函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的偶函数 | D. | 最小正周期为π的偶函数 |
分析 运用向量的数量积的坐标表示和二倍角公式,化简f(x)=-$\frac{1}{2}$sin4x,再由周期公式和奇偶性的定义,即可得到所求结论.
解答 解:由$\overrightarrow a=({2sin2x,-1}),\overrightarrow b=({{{sin}^2}x,sin2x})$,
函数$f(x)=\overrightarrow a•\overrightarrow b$=2sin2xsin2x-sin2x
=sin2x(2sin2x-1)=-sin2xcos2x
=-$\frac{1}{2}$sin4x,
可得最小正周期T=$\frac{2π}{4}$=$\frac{π}{2}$,
由f(-x)=-$\frac{1}{2}$sin(-4x)=$\frac{1}{2}$sin4x,
即有f(x)为奇函数.
故选:A.
点评 本题考查向量的数量积的坐标表示和三角函数的化简,同时考查函数的奇偶性和周期性,属于中档题.

练习册系列答案
相关题目
13.如图是某几何体的三视图,则该几何体的体积为( )


| A. | 24 | B. | 36 | C. | 72 | D. | 144 |
11.一个圆内有一个内接等边三角形,一动点在圆内运动,则此点落在等边三角形内部的概率为( )
| A. | $\frac{3}{π}$ | B. | $\frac{{3\sqrt{3}}}{4π}$ | C. | $\frac{{\sqrt{3}}}{4π}$ | D. | $\frac{{2\sqrt{3}}}{3π}$ |
18.抛物线$y=\frac{1}{2}{x^2}$的焦点坐标是( )
| A. | (0,1) | B. | $({0,\frac{1}{2}})$ | C. | $({0,\frac{1}{4}})$ | D. | $({0,\frac{1}{8}})$ |
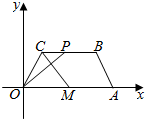 在平面直角坐标系xOy中,已知四边形OABC是等腰梯形,OA∥BC,$A(6,0),C(1,\sqrt{3})$,点M满足$\overrightarrow{OM}=\frac{1}{2}\overrightarrow{OA}$,点P在线段BC上运动(包括端点),如图.
在平面直角坐标系xOy中,已知四边形OABC是等腰梯形,OA∥BC,$A(6,0),C(1,\sqrt{3})$,点M满足$\overrightarrow{OM}=\frac{1}{2}\overrightarrow{OA}$,点P在线段BC上运动(包括端点),如图.